https://www.mathed.page/t-and-m/turtle-and-mouse.html
The Turtle in the Age of the Mouse:
Why I Still Teach Programming (1997)

by Henri Picciotto
The Urban School of San Francisco
My colleagues and I have reserved a significant place in our department's curriculum to the teaching of programming. In this article, I will explain why we have followed a path that has diverged somewhat from the one traveled by the majority of computer-using math teachers. I will summarize the history of our relationship to technology, give examples of some of our students' work in this area, and conclude with some thoughts on the place of programming in education.
For many years, I was a self-taught Logo enthusiast, and incorporated Logo into my school's curriculum in many ways:
- introducing computer programming and algorithmic thinking, as well as recursion and fractals;
- enriching math classes through computer tools I wrote for graphing and geometric constructions, plus games to reinforce number sense (signed numbers, complex numbers) and assorted other understandings (functions, Cartesian and polar coordinates). See Picciotto (1990).
A summary of my involvement with computers up to that point can be found in Picciotto (1989). Since then, there have been many new arrivals on the technology front:
- dynamic geometry (Cabri, Sketchpad)
- the graphing calculator (especially the TI "eighty-something" machines)
- electronic symbol manipulation (most relevantly at the precollege level, the TI-92 and the TI-89)
Less well-known is the development of Boxer, a current representative of the programming / turtle geometry tandem that was made famous by Logo.
I have not yet done much with electronic symbol manipulation, so I will leave it out of this paper. As for the other tools, let me first talk about my own mathematical / technological needs. I think about pedagogical problems much more often than mathematical problems, but once in a while I do come across a mathematical question and concentrate on that for a while. It is interesting to note that when that happens, these days, I almost always reach for one or another technological tool to support my thinking. Two examples: Iterating 2|x|-2, and Mapping Triangles to Points. What these examples show is that in my own mathematical life, I use dynamic geometry, graphing calculators, and programming in Boxer, and I appreciate the fact that I have enough familiarity with them to be able to choose the appropriate one for each situation. At this stage, no one tool addresses all my needs.
My students are less sophisticated mathematically, and they are less familiar with math software. Most of what they know about mathematics or math software, they know because it is part of the curriculum my colleagues and I offer them. Since class time, preparation time, and student attention are limited, we must make some choices.
Over the years, in the informal competition between various electronic classroom tools, the graphing calculator has proven to be the winner by far. My students have developed much more of a sense of ownership of that technology, my colleagues likewise, and the profession as a whole has adopted these devices in a way that no computer software can compete with. I suspect that the reasons for this success are:
- the machines are relatively inexpensive
- they can be carried in a backpack, and used anywhere
- they are user-friendly
- there is a good match between the capabilities of the graphing calculator and a wide range of mathematical topics we teach
The last two points are the result of careful work on the part of the designers, who have genuinely listened to math educators. The result is that the question is no longer whether to use the graphing calculator, but how to do it: the TI-83 or equivalent is now a given in the classroom of most technology-savvy teachers. In my own classes, and those of my colleagues at the Urban School of San Francisco, the TI calculators have proven themselves to be an excellent replacement for my Logo Grapher program.
But what about the other uses we made of Logo in the eighties? In order to build on that work, we have replaced Logo with Boxer. Boxer is a new computer language, or as its creators describe it, a computational medium. It is an attempt to make programming accessible; to make it easy to integrate programming with the learning of subject matter; and to make it easy for teachers to build computer tools. Its development is led by Professor Andy diSessa at UC Berkeley, and we have had an opportunity to use it at the Urban School.
The games, while they were quite effective, have vanished from our curriculum, because I didn't take the time to write a Boxer version of them. (However should I decide to build a Boxer version of the games, it should be a manageable task. Boxer is a great environment for the teacher or student as programmer of tools and games -- see some examples below.) In Boxer, the introduction to programming, the geometric construction work, and the work with fractals has been made accessible to more students than it ever had been with Logo. In the remainder of this paper, I will describe some of this work.
Many teachers have been turned off to teaching programming by the high overhead involved in learning programming languages for both teacher and student. As a result of early negative experiences along these lines, or because they fear having those experiences, most math teachers have stayed away from programming. In part, this reflects the limitations of the computer languages that have been available to the education community.
We introduce all of our students to programming using Boxer in a required math course ("Math 2"), which replaces the traditional Geometry course. To do this, we use turtle geometry challenges in the Logo tradition (many books on Logo from the eighties include such lessons). The motion of the turtle provides a concrete manifestation of the program's code, thereby providing students with an "object to think with" to use Logo inventor Seymour Papert's phrase. However Boxer's design incorporates some fundamental improvements on Logo, many stemming from an intelligent use of the two-dimensional graphical displays now available, as opposed to the one-dimensional teletype displays Logo was originally created for:
- variables are visible: they are labeled boxes on the screen -- this makes it much easier for beginners to understand what is happening when a program is run, as the contents of variables can be inspected or modified at all times
- programs are visible, in "doit" boxes on the screen -- debugging can be done by executing each line of the program by double-clicking on it
- comments and other text can be placed in data boxes anywhere, among various other kinds of boxes, including graphics/ boxes, turtle boxes, and more
Every box (variable or program) can be "seen" locally or globally, depending on where it is placed by the user, who can organize the workspace as he or she sees fit. Each box can be expanded or shrunk, and boxes can be nested arbitrarily deep.
Several views of a typical student "world" are shown in Figure 1.
Figure 1a: The MENU box contains a list of programs written by this student. The programs, as well as other menus, reside in "super-shrunk" boxes, which appear as tiny squares ( ).
).
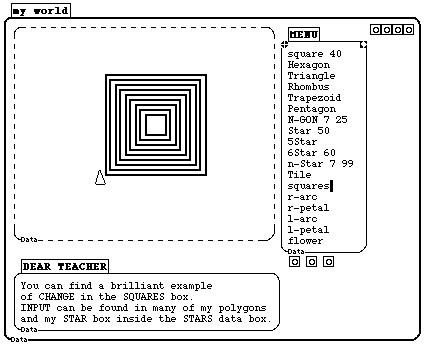
Figure 1b: The box POLYGONS can be found in one of the super-shrunk boxes of Figure 1a. Squares is the procedure that created the image in Figure 1a. It uses a variable (x) and the subprocedure SQUARE.
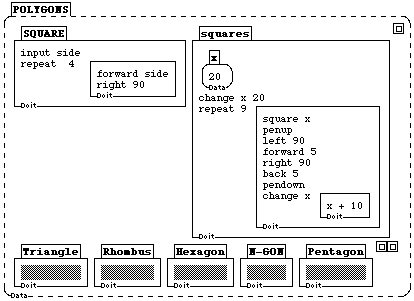
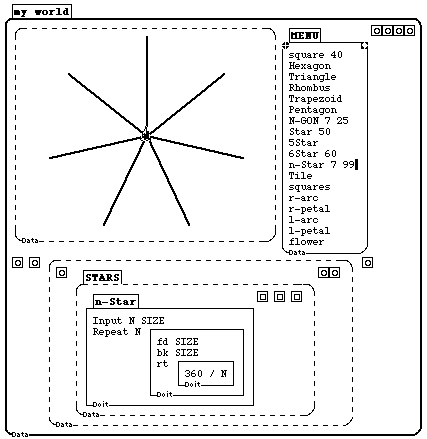
Figure 1c: n-Star is a procedure with two inputs.
Programming is a field that lends itself uniquely well to projects and creativity. Any assignment can be embellished. Several students in each class come up with their own ideas, and pursue them, sometimes for months. The Logo slogan ("no threshold, no ceiling") definitely carries over to Boxer, only it is even more applicable. Whereas only a handful of "computer jocks" can produce interesting programs in a language like Pascal or C, just about every student in my small school is able to write simple but interesting programs like the ones in Figure 1. On the other hand, Boxer does not limit the more advanced programmers: these students are able to go much further and do some fairly sophisticated work. Examples of boxes created by students with special talent and/or tenacity are shown in Figure 2.
Figure 2a: This is one frame of a comic strip that was created by a student who combined turtle graphics/ with some freehand drawing with the mouse, using a simple "paint" program she wrote.

Figure 2b: This box is self-explanatory.
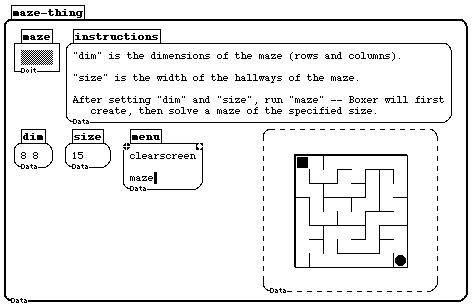
Figure 2c: This is the actual maze program. Boxer makes it possible to inspect a program at any level of detail, by shrinking and expanding boxes accordingly. The student organized its modules logically to facilitate this. The large scale structure of the program consists of four calls: setup, the-loop, solve-setup, and solve. The subprocedures of the-loop, for example, are placed next to it. Shared subprocedures and variables are at the bottom. Note that the variables in this case are numbers, arrays of numbers, colors, and in the case of can-goes, a three-dimensional Boolean array.
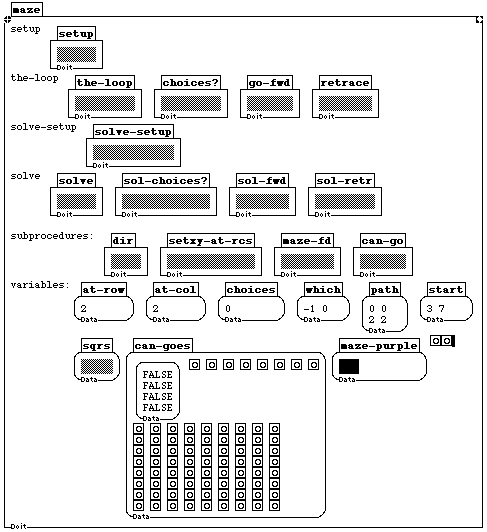
Figure 2d: This program illustrates the intersection of a cube and a plane.
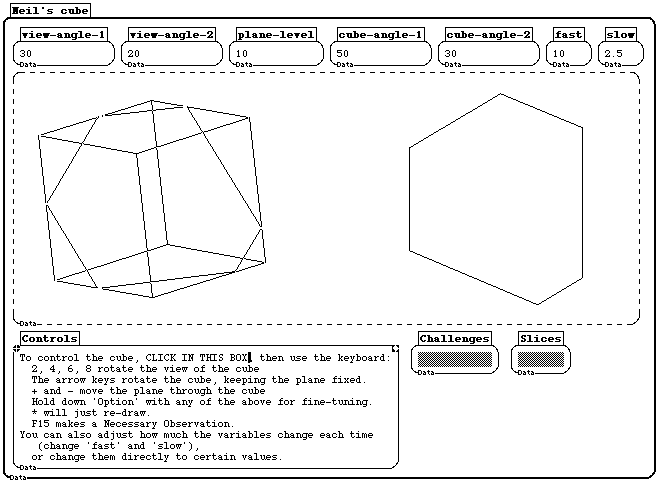
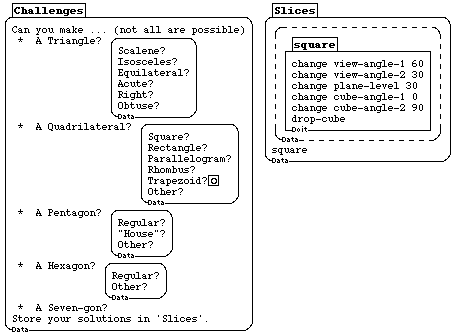
Figure 2e: The cube program in Figure 2d was written by a senior. I now use it in my classes, because it includes challenges for the user. The square procedure can be copied and edited to build a library of answers to the challenges. In the classroom, students use a physical cube made from a transparency, with the sections made from stiff paper for their initial exploration, and then continue with the help of the program. This activity is great for 3D visualization, and leads to great projects (proofs of impossibility, physical models of different slices, finding the largest figure of each type, and so on.)
In the first trimester of Math 2, we use turtle geometry activities, which reinforce the concept of angle and allow for an exploration of the sum of the angles in a polygon. The boxes in Figure 1 came out of that phase of the course. In the second trimester, we use a teacher-created program (called Geometer -- see Figure 3). This environment compares favorably with something like the Geometry Supposer, but is inferior to Cabri or Geometer's Sketchpad. Still, it helps to get many important and interesting ideas across, particularly in construction challenges, or to a lesser extent in the generation of conjectures. Once a construction has been achieved, it can be replayed over and over, with different initial points, or manipulated simply by dragging the initial points.
Typical assignments are: construction of tangent lines and circles in various situations; writing procedures to draw triangles given three sides (SSS), two sides and the angle between them (SAS), or two angles and the side between them (ASA); writing procedures to construct various quadrilaterals, and discussion of the number of inputs required, and which procedures can construct which figures. For example, the parallelogram procedure requires three inputs, and with appropriate values for these inputs, can be used to also draw a square, a rectangle, or a rhombus. This reveals concretely the logical relationships between the figures.
Geometer was programmed by a few people in their spare time, rather than by professional programmers over several years. The result was a nice chunk of the instructional functionality with a huge amount less programming effort. This is a big benefit if you believe (like the creators of Boxer do) that teachers and students need a wide variety of kinds of software rather than just a few applications. Boxer can be used to develop useful learning tools for number theory, for probability and statistics, for physics, and so on. While each Boxer tool is inferior to a comparable commercial product, it is relatively easy to create and modify (by the teacher), and it is completely programmable (by the students). Once students know the basics of Boxer programming, they can write program in Geometer or in any of the other Boxer tools. Theoretically, this can lead to a programming-centered, tool-rich culture in schools. Practically, we're not there yet, but I'd like to describe some glimpses I've had of such a culture.
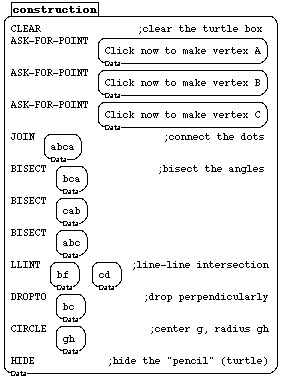
Figure 3a: Commands can be used by double-clicking on them or by including them in procedures. Double-clicking can automatically build a written record of the construction (see Figure 3b), which can be inspected, edited, saved, accessed and executed later. The boxed points (a, b, c) are the initial points, and can be dragged, in the style of much fancier dynamic geometry software.
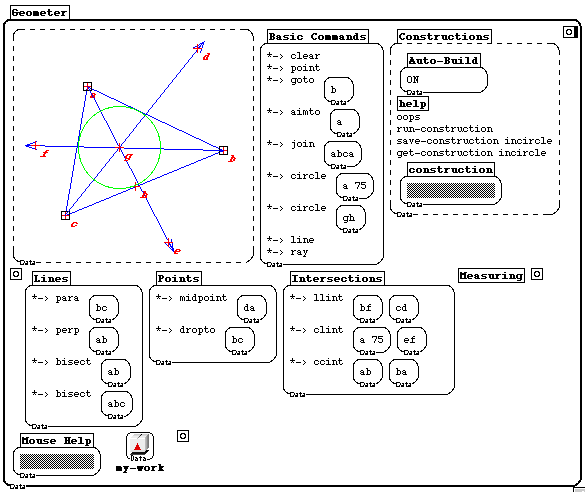
Figure 3b: Here is the construction that yielded the figure in 3a. It was saved automatically by the program. The comments were added later.
My best experience with the kind of synergy that is possible when programming meets mathematics was in a class called "Infinity". In this ten-week course, we used Boxer to learn about iterating functions, and about self-similar fractal figures. (There were other topics in the course, but I will only address the ones that involved Boxer.) A few students had used Logo in the past, but most had no prior experience with programming. The class consisted of two sophomores, a dozen juniors, and one senior. Only one sophomore and the senior could be considered to be top-track math students (as measured for example by whether they took calculus in their senior year.) Among the rest, all had completed two years of high school algebra and took this class as their last math class. In short, most can be considered average college-bound students (though one ended up not going to college, and another went to a community college).
I dwell on the composition of the class because I was stunned by the high level of achievement in the two areas where Boxer was used. After a brief introduction to Boxer, we investigated the iteration of functions by way of programming procedures that would build tables to show the value of the function after a given number of iterations. In other words, very early on, we tackled the sort of programming (list manipulation) which I was only able to introduce to tiny numbers of students in my Logo days. Moreover, the mathematical payoff was enormous. We experimented with various functions in a way that clarified the meaning of composition, iteration, and recursion, and we compared algebraic methods to analyze those phenomena with computational ones. This work made it possible to have an unusually effective introduction to mathematical induction. In particular, we used Boxer to experiment with the chaotic iteration of non-linear functions. (The Iterating 2|x|-2 problem originated at that time, but I worked on it long after the class was over.)
Later, students were introduced to basic turtle graphic commands, and to a series of templates of programs to generate self-similar figures. Within a few weeks, all students without exception had created strikingly beautiful and complex fractals as their final project., with broad variation among them. See Figure 4 for a few samples. In addition to the programs, students were expected to analyze the mathematics of the images they created, including its dimensionality and the total distance traveled by the turtle in creating the image. Again, this was a level of work I was only able to get out of very few in my Logo days: using recursive structures in programs had seemed to be only accessible to the very top students.
I could have used a ready-made fractal-generating program for this part of the course, though I am not sure it would have been possible to create figures like the ones in Figure 4 with that approach. I could have used spreadsheets for the work on iteration. However, the students would not have nearly the depth of understanding they were able to gain by doing their own programming. Besides, the "overhead" that is the necessary component of learning any software starts to add up if you always use a different piece of software for each task. Boxer made it possible to have a unified electronic environment throughout the course. Whatever interface quirk or programming construct was learned in one context was easy to transport to another, which contributed to substantial savings in overhead.
Figure 4a: The same student-written fractal tree program, with different degrees of symmetry, and at different levels, produced all these images.
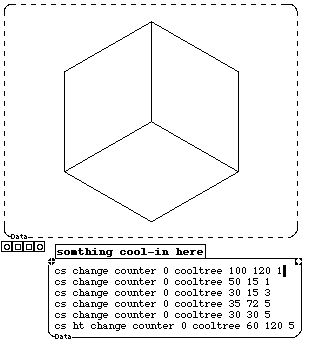
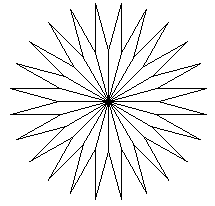

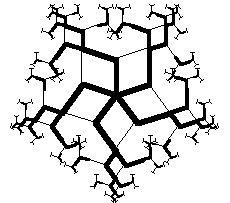

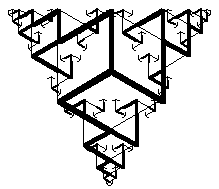
Figure 5b: This student included her mathematical comments (including the dimensionality of the fractal and the number of cross-shaped "voids" at level n) in the boxes under the image.
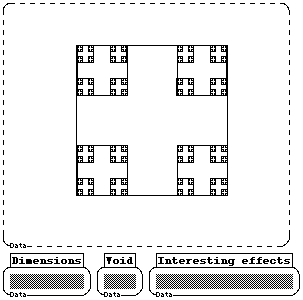
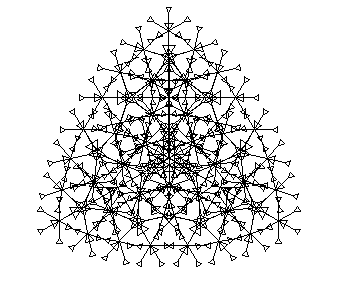
Figure 5c: This complex and beautiful mathematical object was invented by a student in the Infinity class. Overall, it has three-fold symmetry, but upon close inspection, you will find four-, five-, and six-fold symmetries locally. The program that created it allows you to "zoom" into any of the local centers of symmetry, and create a full-sized representation of it.
The work we have done in Boxer in the past few years has been partially successful, as evidenced by the student work shown above. However, we have experienced a fair amount of frustration along the way, and cannot really claim total success. There has been much resistance to Boxer from many students. This can be partially explained by its early tendency to crash a lot, which caused students to lose much work through no fault of their own. In addition, there were a number of weaknesses in the interface, which originated on UNIX workstations, and for a long time differed markedly from what students expected from their use with other software on the Macintoshes we have been using. As a result of student frustration, it has not been easy to "sell" it to my colleagues. Fortunately, Boxer is now more stable, and its interface much more Mac-like.
Another partial explanation of the difficulties we encountered is that many students come to the course with negative prejudices about programming. In our culture, the stereotype of the nerdy programmer is perhaps even more widespread and negative than the stereotype of the geeky mathematician. People never tire of saying that you don't need to understand electricity to turn on the light, and that similarly, you don't need to understand programming to use a computer. (This is of course true, but no one seems to object to teaching our students about electricity.) The software industry, well aware of the cultural bias, tries to avoid even the word "programming" when addressing their customers. For example, most fairly complicated applications allow the user to create "macros" or "scripts". Applications are programs, macros are programs, and scripts are programs --but the euphemisms reign.
And yet, programming offers an extension of our brain in a way that qualifies it as a new level of literacy, with broad applicability to many fields. There is power in understanding algorithms. The programmer's habits of mind (breaking down large tasks into small ones; thinking about structure hierarchically and logically; seeking clarity in presentation and precision in language; and so on) are useful in a wide range of human activity, especially mathematics. Math education certainly has been transformed by access to programming. (Heck, there would be no graphing calculators or dynamic geometry software without programmers!) And in contemporary mathematical research, computers are used routinely in a very broad range of fields: number theory, topology, combinatorics, and so on. Programming is the most creative activity one can have at the computer, and it is wrong to reserve this for a tiny minority of our students.
There was a time when reading, writing, and arithmetic were not taught to all. They are now seen as part of basic skills we expect of all citizens. We are beginning to try to teach algebra to all students. Should programming be part of every student's curriculum? I certainly hope that this question comes back to the fore in our discussions. In any case, we should avoid faddishness. Our technological choices need not change as fast as the technology does. Reflection and discussion about mathematical and pedagogical questions ought to be our guide. My students can learn from all of the tools discussed in this paper, just like I can -- the question is how to achieve the right balance within an over-full curriculum. Hopefully, as software and high level programming environments such as Boxer become easier to use, and computers are more ubiquitous and less expensive, it will become possible to include more and more technological strands in the educational fabric.
The samples of student work include creations of Neil Picciotto, Christian Utzman, Lauren Veen, and other students at the Urban School.
Henri Picciotto, Bruce Sherin, Andy diSessa co-authored the Geometer program. Neil Picciotto added a feature.
Neil Picciotto and Bruce Sherin provided useful comments on a draft of this paper.
Bibliography
Henri Picciotto: "Teacher-Created Educational Software: BASIC, Logo, Boxer" (Technical Report E4, the Boxer Group, Graduate School of Education, University of California, Berkeley, 1989)
Henri Picciotto: Logo Math: Tools and Games, a comprehensive computer environment to enhance the discovery-based learning of secondary school mathematics (Terrapin, Inc., Cambridge, MA, 1990)


















