If you have the Cabri 3D software (or the free evaluation version), you can make your own figure by following along. You can also download my figures. All of them are zipped together in this archive -- but in fact, they are all based on the same original figure.
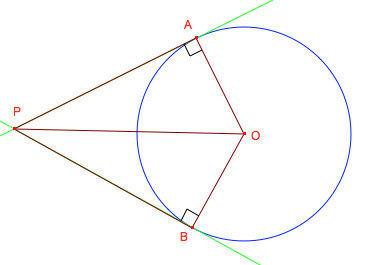
In this page, I will present a proof that the intersection of a cone and a plane can be an ellipse. The proof is based on basic 2D geometry. We'll need the fact that two tangents to a circle have equal lengths. This is easy to prove in the figure below, and the same argument can be used to show that this remains true in the case of tangents to a sphere:
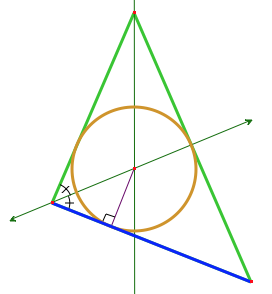
We'll also need to know how to construct a circle tangent to three lines, using angle bisectors, and dropping a perpendicular to get the radius:
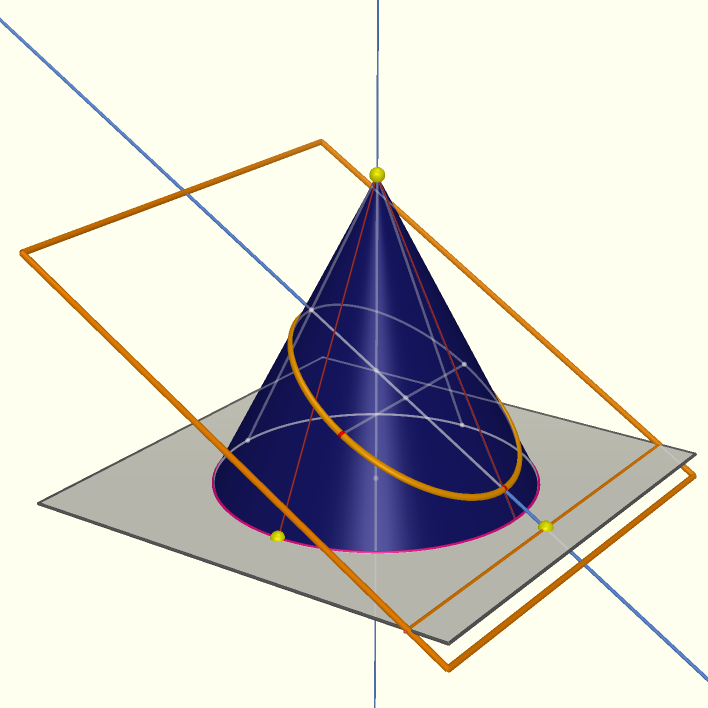
We will construct two spheres that are each tangent to both the cone and the plane. Clearly, the center of such a sphere must be on the axis of symmetry of the cone, but where on the axis? Looking at the figure a different way suggests that this problem is not unlike finding the center of the circle inscribed in triangle RSV:
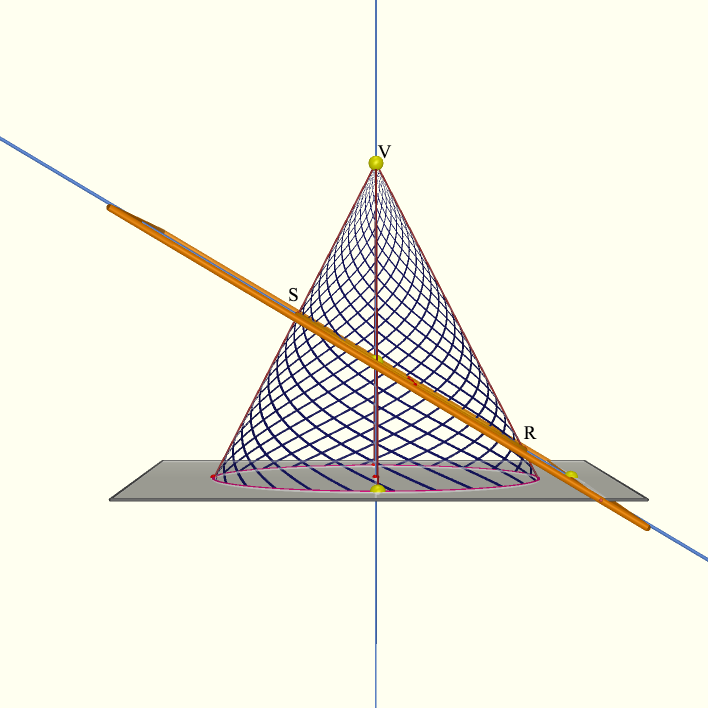
(Of course, this will only work if this triangle exists. If it doesn't, we won't have an ellipse.) To find R and S, find the intersection of the plane with a plane that is perpendicular to the cone's axis of symmetry (e.g. the base of the cone.) Construct a plane through the axis of symmetry, perpendicular to that line. R and S are its intersections with the intersection curve.
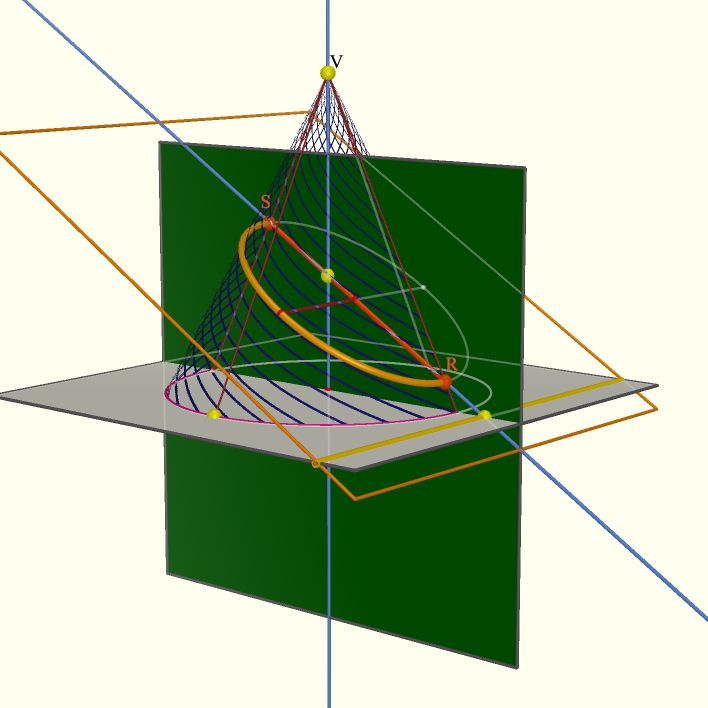
The center of the sphere is at the intersection of b, the plane that bisects ∠RSV, and the cone's axis of symmetry. To find the radius of the sphere, drop a perpendicular (h) onto the original plane:
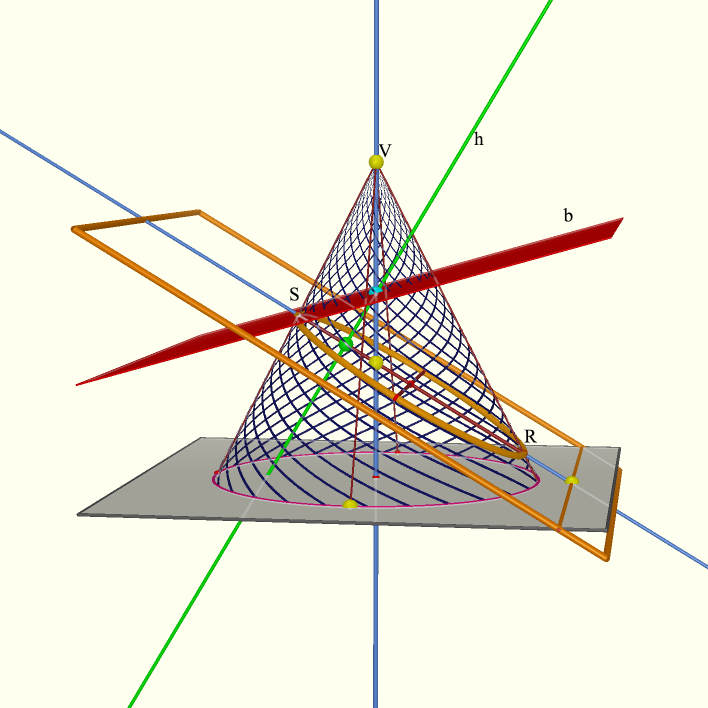
The sphere touches the cone along a circle, and the plane at a point:
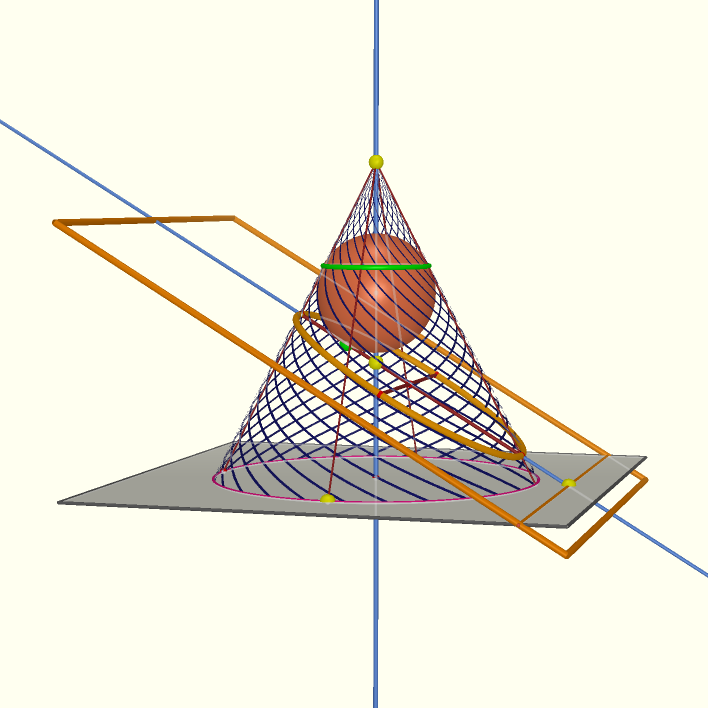
Do this again on the other side of the plane:
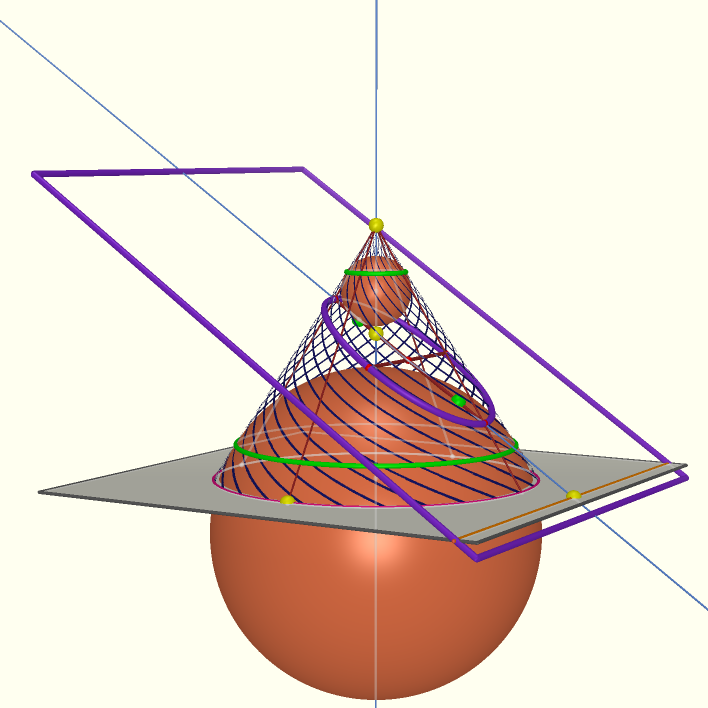
Let us call the points of tangency between the spheres and the plane F1 and F2.
We are now ready for the proof. Consider a generic point P on the intersection curve. Draw the line PV. It will intersect the circles at points S and T.
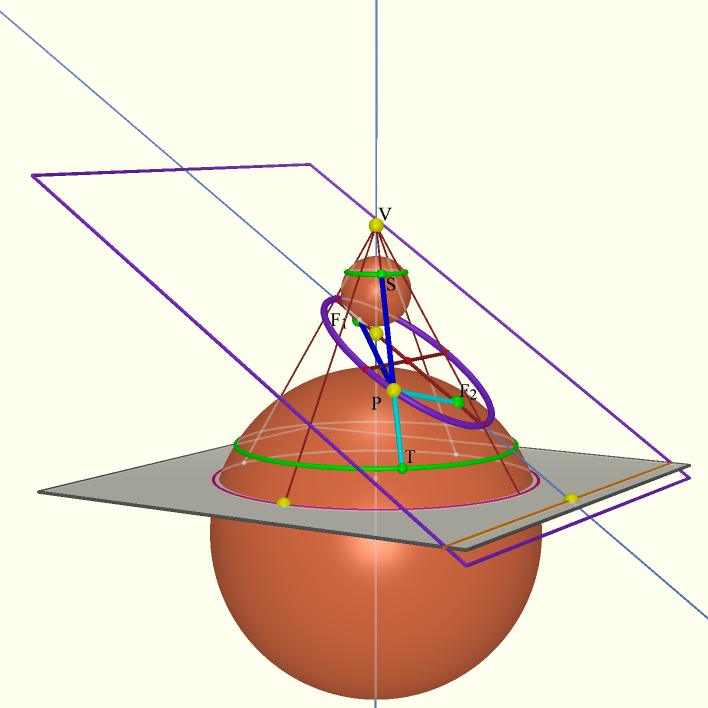
PS = PF1 because both segments are tangents from P to the sphere. Likewise, PT = PF2. Therefore, PF1 + PF2 = PS + PT. But PS + PT = ST is constant, no matter where P lies on the curve. Therefore, the sum of the distances from P to F1 and F2 is constant, and P is on the ellipse with foci F1 and F2. QED.
The same argument can be made in the case of a plane slicing through a cylinder:
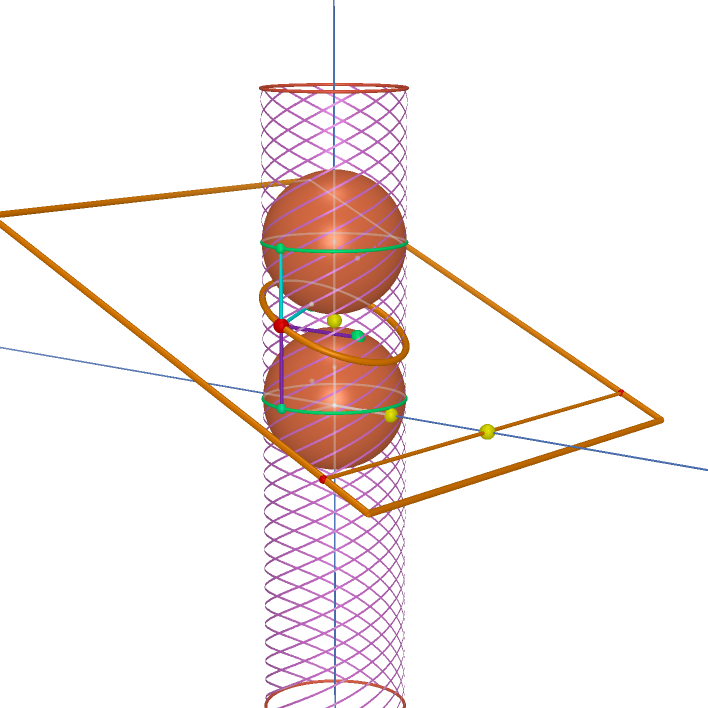
(Download the file.)