The Problem
Soccer (football, outside the US) provides us with an interesting question. Imagine a player running towards the goal, in a line perpendicular to it. Assume this is a drill, and there is no one guarding the goal. Assume also the player is so strong that distance from the goal is not an issue. At any given time, the player is at the vertex of a shooting angle, with the sides of the angle passing through the goalposts. If he (or she) shoots within the angle, he will make the goal. Outside, he will miss. Clearly, a bigger angle is better.
The above figure is interactive: you can move the player along the line. Note that as he runs towards the goal, the shooting angle starts out small, increases as he gets closer, but then gets small again as he gets close to the goal line. The optimal shot is somewhere between the extremes. But where?
Note that the angles on a given circle through the goalposts stay constant, but changes if the circle changes (you can move the player around the circle; to change the circle, move its center):
In fact, as our player runs down the line, his shooting angle is less than the circle's shooting angle when he is outside, and greater when he is inside:
This suggests that the optimal point is given by the circle through the goalposts that is tangent to the line:
The Solution
The following figure suggests a construction for the tangent circle, and thus for the optimal point:
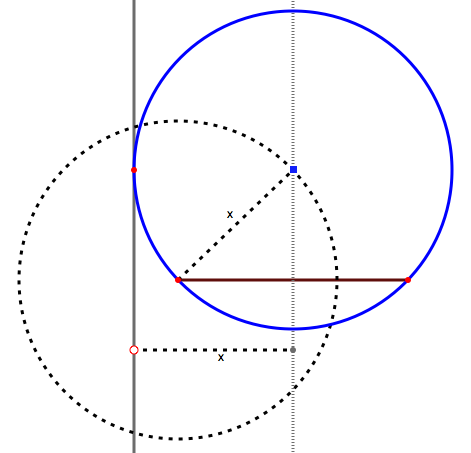
(Explanation: if the circle passes through the goalposts, its center is on their perpendicular bisector. But where? If it is tangent to the line, and the line is at a distance x from the bisector, then the center is at a distance x from the line, and from the goalposts. Therefore it is on a circle centered at either one of the goalposts, with radius x.)
Interestingly, the locus of the optimal points (as x varies) is a hyperbola:
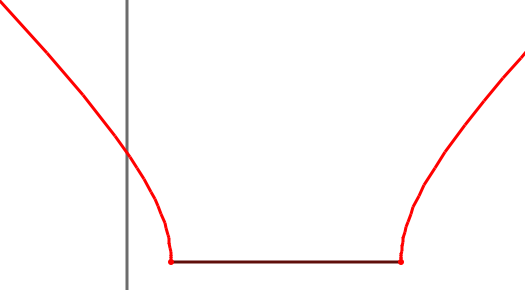
This is easy to prove. Assume the origin is the midpoint of the goal, and the goal has width 2:
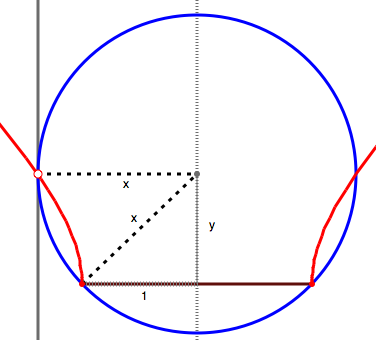
By the Pythagorean theorem, y2+1=x2, but (x,y) is the optimal point. Since it's coordinates satisfy the equation x2-y2=1, it lies on a rectangular hyperbola.
All the above figures were created using this GeoGebra file.
Generalizing
What if the line is not perpendicular to the goal? Much of the argument is the same, but I could not find a straightedge and compass construction for the tangent circle. (Dan Bennett found one, which I share below, at the end of this article.)
Note that the center of the needed circle is equidistant from the line and each of the goalposts. Therefore, it lies on the parabola that has one of the goalposts for its focus, and the line for its directrix:
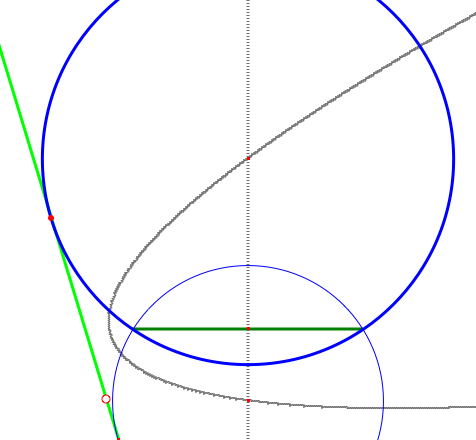
The center, therefore, is at the intersection of the parabola and the goal's perpendicular bisector. Interestingly, the locus of the optimal points, for a given angle between our line and the goal, seems to still be a rectangular hyperbola:
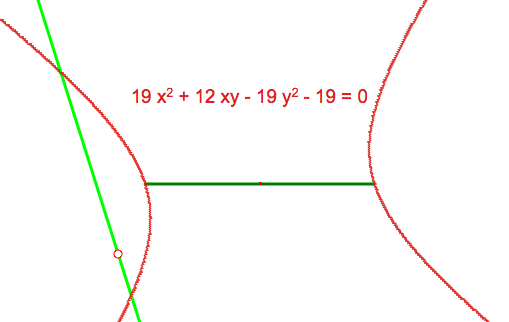
Note that Cabri gives the equation of the curve -- which of course is not a proof, but it does offer encouragement for this conjecture. In fact, the software allows you to change your axes:
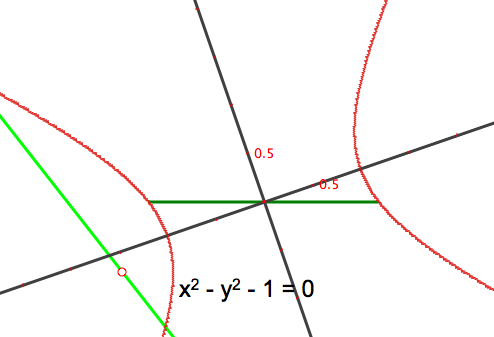
With these axes, the equation is readily recognizable.
One more interesting locus: as the angle between the line and the goal changes, what is the locus of the hyperbolas' vertices? It seems to be a lemniscate:
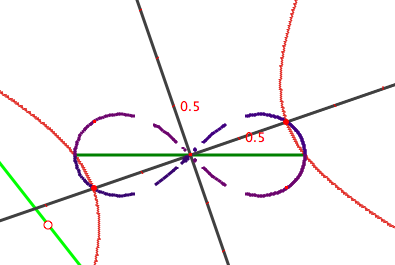
Compass and Straightedge Construction
Dan Bennett's construction for the generalized soccer problem does not require a parabola. Instead, he makes clever use of dilation and similar triangles. The first step is straightforward — construct a circle tangent to the goal and the runner's line:
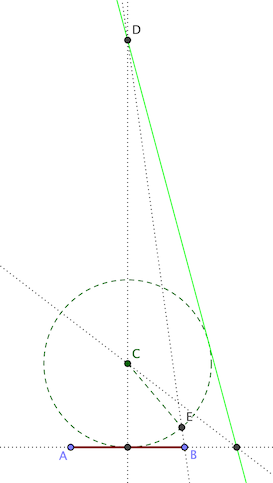
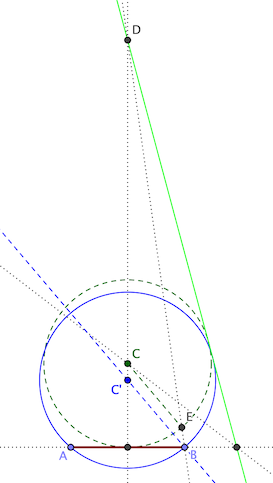
In the figure: C is the circle's center; D is the intersection of the runner's line L with the goal AB's perpendicular bisector; E is an intersection of the circle with DB.
The needed circle passes through A and B, and is tangent to L. We can find its center with an appropriate dilation centered at D. Such a dilation would keep the center on CD, and preserve the tangency with L. All we need is the appropriate ratio.
Draw a parallel to CE through B. It meets CD at a point C'. ∆DCE and ∆DC'B are similar, so `\frac{DC'}{DC} = \frac{DB}{DE}`. Therefore, the circle through B, centered at C' is the needed dilation of the original circle.

