Five months have passed since the last issue of this newsletter. I had a busy summer which included teaching workshops on both coasts. Then in September, I did some vacationing. Somehow, I managed to continue blogging, and I added some new materials to my Web site. As a result, I have some possibly useful links for you.
Let's get started!

Blog Posts
Here are links to posts on my Math Education Blog that you might find interesting.
If you are so moved, you may comment on the posts, and/or subscribe to the blog.
Two More Puzzles on a Lattice
First: find all the triangles with area 15 on a standard 11 by 11 geoboard. If one or two sides are horizontal or vertical, this is not difficult, but it directly leads to understanding strategies and formulas to find the area of a triangle. I have used versions of this for a long time. But while preparing a workshop, it occurred to me to look for triangles with area 15 with no horizontal or vertical sides. That's a lot harder! Read about it here.
Second: "Ariadne's String". You must navigate from one given lattice point to another by following a strict set of rules. A fun and challenging application of the Pythagorean theorem. Read about it here.
Themed Courses?
What are the pros and cons of courses with a theme, such as "Trigonometry", as compared to courses that range over many themes, such as "Math 3"? As I see it, this is not a matter of principle, but needs to be discussed case by case. I give examples from my experience when I taught high school. Read about it here.
Perpendicular Bisector Theorem
This is another post in my ongoing series about transformational geometry. The Common Core requires us to prove SSS, SAS, and ASA on a foundation of transformations. To do that requires among other things proving the properties of the perpendicular bisector of a line segment. Read about my suggested approach here.
MathEducation.page
New(ish) on my Web site.
Exponential Functions
A launch page for three activities about exponential functions.
- Rolling Dice
- An anchor lab, using ten-sided dice, which I have often used on day 1 of Algebra 2. It is a powerful modeling lesson which has been on my site since 2002, if not earlier. It appeared almost verbatim in the Mathematics Teacher not long ago, and a similar activity has recently been published by the Illustrative Mathematics folk. Good ideas ripple out!
- Exponential Graphs
- These are almost purely visual worksheets, where students must deduce the formula for each graph, and along the way develop some understanding about key properties.
- Exponential Graph Similarity
- A worksheet for teachers, wherein you will discover that all exponential graphs are similar. (Yes, similar in the math sense of the word.)
Constant Sums, Constant Products
A launch page for "Constant Sums, Constant Products," an untraditional approach to traditional topics. It is a mega-unit, spanning content from middle school, all the way to what one might call "teachers' mathematics." Take a look at it when you have a little time to devote to it. The unit is based on material from Algebra: Themes, Tools, Concepts (free download: ATTC), and it goes further, ending with an original proof of the quadratic formula.
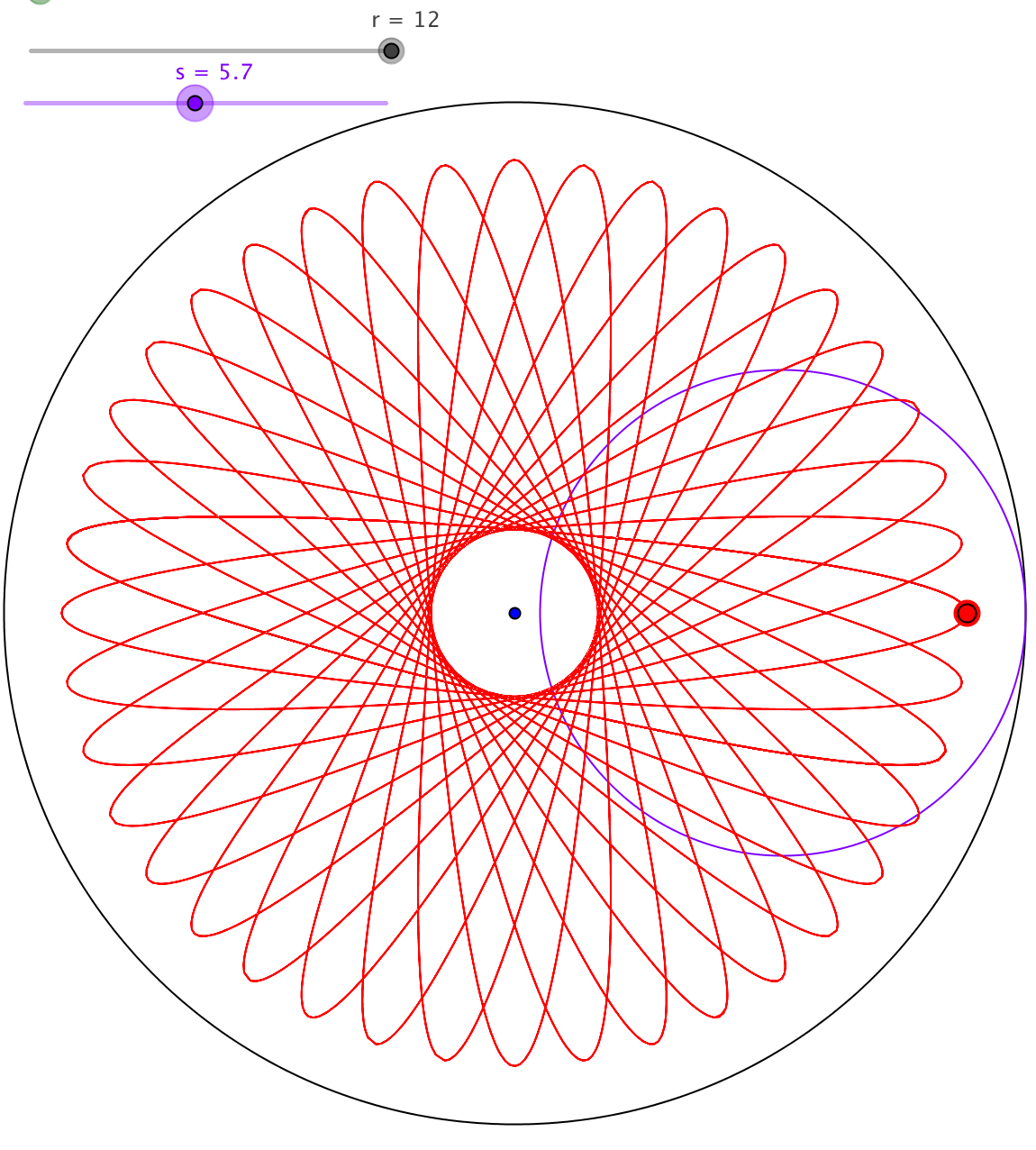
Spirograph Simulation
Some mathematical and artistic fun with a spirograph simulation. How are the radii related to the symmetries of the resulting figure?