Introduction
Geometry Labs is a book of hands-on activities that use manipulatives to teach important ideas in geometry. These 78 activities have enough depth to provide excellent opportunities for discussion and reflection in both middle school and high school classrooms.
- Middle school teachers will find many labs that help prepare students for high school geometry by getting them to think visually and become familiar with fundamental concepts, figures, and vocabulary.
- Teachers of high school geometry —whether traditional, inductive, or technology-based— will find many labs that approach key topics in their curriculum from a different point of view. In some cases, the labs in this book can replace corresponding lessons in your textbook. Other labs can be used to preview or review material that you teach in more traditional ways.
- Trigonometry teachers will find a new approach, using the CircleTrig geoboard, to introduce basic right-triangle and unit-circle trigonometry concepts. This approach also makes trigonometry accessible to younger students.
- Most of the labs include a discussion section. Those questions often make it possible to get at important ideas, especially if you use them to structure whole-class and/or small group conversations, or as prompts for student writing.
You may download the whole book or individual sections
for your non-commercial use.
For a preview of some labs from the book, see:
Manipulatives
Most of the labs require the use of manipulative materials: tangrams, pattern blocks, cubes, mirrors, and two manipulatives I designed, the CircleTrig Geoboard, and the Geometry Labs Template. This is not because hands-on activities magically confer understanding! The idea is to use those labs to trigger reflection and discussion. If you don't have the manipulatives, I encourage you to get them — you won't regret it, and your students will be grateful.

CircleTrig Geoboard
On one side, an 11 by 11 geoboard. Useful for many things, especially activities about slope, area, distance, the Pythagorean theorem, and simplifying radicals. On the other side, a circle geoboard, with radius 10 cm, and a 360° protractor. Useful for activities leading to the inscribed angle theorem, and to introduce basic trig, both on the unit circle (the unit being the decimeter) and in right triangles. Most of these activities of course can be done on paper, but it's more fun to start on the geoboard.
Virtual 11 by 11 Geoboard | Virtual Circle Geoboard
(Where to purchase the CircleTrig Geoboard.)
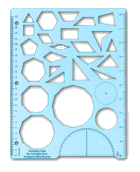
Geometry Labs Template
Eight different triangles, ten different quadrilaterals, seven different regular polygons, and all the pattern blocks — shapes you need for basic geometry activities. The template is great for exploring tilings (tessellations). It also includes centimeter and inch rulers, plus a numberless protractor. You can keep it in a 3-ring binder. See it as a PDF.
The template is also useful in introducing translations, reflections, and rotations. See this unit.
Individual Sections
Connections, Corrections, Extensions, and Revisions(See also the teacher notes at the end of the book.)
You are welcome to contribute to this page. Email me.
- Table of contents, Introduction
- A correlation of many Labs with the topics they support, by Mimi Yang.
- Section 1: Angles
- Google slide for group record-keeping of Lab 1.1 (Angles Around a Point)
- I've used Lab 1.1 as a Day 1 activity for my Geometry class, many times.
- Alternate version of Lab 1.1, by Liz Caffrey
- Alternate version of Lab 1.3 (Clock Angles), by Liz Caffrey
- Possible intro to Lab 1.7 (Angles and Triangles in a Circle), by Michael Pershan.
- Consider doing Lab 1.10 (Soccer Angles) before Lab 1.7, as suggested by Alex Wilson.
- Extension of Lab 1.10 (Soccer Angles), using interactive geometry software.
- Section 2: Tangrams
- Possible preview: Tearing Tangrams
- Virtual tangrams
- Solution to part of Lab 2.5: the 14 convex 7-tangram figures
- Extension to Lab 2.5: I discuss convex tangram `n`-gons on my blog
- Section 3: Polygons
- Add patty paper to the "Equipment" for Labs 3.1 and 3.2.
- The "walking" labs (3.3-3.6) work well with programming turtle graphics in Scratch or Snap.
- Correction to the Lab 3.9 solution, by Austin Shapiro and his students at Proof School, SF
- (Lab 3.9 itself has now been corrected. The above only applies if you used its original version.)
- Section 4: Polyominoes
- Virtual Grid Paper
- Extension of Lab 4.7 (Minimum Covers), on my blog.
- A book of Polyomino Lessons (Some overlap with this section.)
- More on polyforms: Geometric Puzzles in the Classroom
- Geometric Puzzles Home Page
- Section 5: Symmetry
- Slight edit of Lab 5.6, an attempt to make the table headings easier to understand.
- Online applet to support Lab 5.6: Symmetry with Pattern Blocks
- Some Lab 5.6 photos for discussion.
- Extension of Lab 5.6: Cover the Big Dodecagon with pattern blocks, + connections.
- Symmetry Home Page
- Online unit: Symmetry Labs
- Section 6: Triangles and Quadrilaterals
- Lab 6.1: Use patty paper! Have students share the work and report what they discover.
- Lab 6.2 (Walking Parallelograms) works well with turtle graphics in Scratch or Snap.
- John Golden's GeoGebra version of Lab 6.4: Making Quadrilaterals from Triangles
- Section 7: Tiling
- Virtual tiles for Lab 7.3: Triangles and Quadrilaterals
- Labs 7.3 and 7.4 can be done early in the year. See this blog post.
- Tiling Home Page
- Section 8: Perimeter and Area
- I've used Lab 8.1 on Day 1 of Algebra 1, and in many other contexts.
- Connection to Lab 8.4 or 8.6: Heilbronn's Triangle
- Extension to Lab 8.5: Inscribing Geoboard Squares in Polyominoes
- Extension to Lab 8.6: Proof of Pick's Formula
- Section 9: Distance and Square Root
- Revision and extension of Labs 9.1 and 9.6: Taxicab Geometry
- Preview or review of Lab 9.2: Pythagorean Theorem home page
- Desmos version of Labs 9.3 and 9.4, by Liz Caffrey
- Lab 9.4 is a great example of non-random drill.
- Extension to Lab 9.4: Ariadne's String
- Section 10: Similarity and Scaling
- Extension to Lab 10.2, #4: Include "tilted" rectangles in your search.
- Connection to Lab 10.2, #5: No Three on a Line
- Different version of Lab 10.4: Rep-Tiles, including an extension.
- Extension to Section 10: Shrinky Dinks, by Rachel Chou (requires cm grid paper)
- Section 11: Angles and Ratios
- Trig intro: I now do 11.2 with the 10-cm circle before 11.1, and 11.5 before 11.4 (more info).
- Connection and slides for Lab 11.8: π for circles, π for polygons?
- Notes, Special Papers, and Answers
- Virtual Grid Paper | Virtual Geoboard | Virtual Circle Geoboard
- 10cm Circle (PDF), to do Chapter 11 on paper.
- 10cm Circle in Cabri, and Sketchpad. (The latter contributed by Roger Gemberling.)
