One day in the late 80's, I asked myself "if you were a bug in the plane, where would you have to stand for a given scalene triangle to appear to be isosceles?" In other words, given a triangle ABC, where are the points P such that (say) ∠APB=∠BPC? I called such points "equiangular points" for the given triangle, and investigated them with the help of a program I created in the Logo programming language.
I liked the figure I created in this process, and used it on the cover of my 1990 book Logo Math: Tools and Games. (See the figure above.) Notice that the locus of the points includes many parts. The easiest to understand are the straight-line extensions of each of the three sides, but it includes other curves. Also notice that in the figure above, there is a point inside the triangle, at the intersection of three curves, from where it appears equilateral.
In 1993, this problem (under the excellent name "Henri's Problem") was discussed at an international gathering of academics about "Computers and Exploratory Learning" in Asilomar, CA. They used it as a way to compare different software tools (spreadsheets, the programming language Boxer, the interactive geometry program Cabri, and others.) Cabri was the clear winner of the comparison, in my opinion, as it allowed for a construction of the curves, and moreover revealed that the curves are cubics, as you can see in this figure:
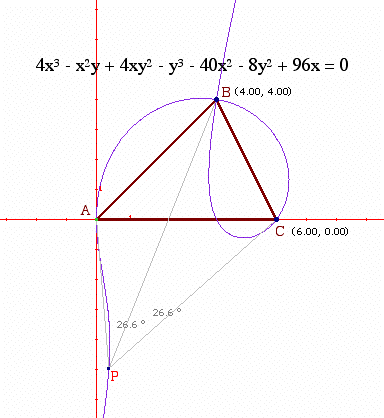
(As far as I know, Cabri is the only interactive geometry application that will give a formula for any locus that was constructed by geometric means.)
However, note that on parts of the curve, the angles in question are supplementary, not equal -- a consequence of the way I constructed it. (If you have a better construction, let me know!) Here is a manipulable figure: you can change the shape of the triangle by moving point C, and you can move P and Q along the locus, which I constructed in two pieces.
(Download the GeoGebra file.)
At some point in the 90's, Jean-Marie Laborde (creator of Cabri) informed me that the problem had been solved by an Italian mathematician who proved that the locus is indeed a cubic.
In July 2006, I attended the Park City Mathematics Institute, a rather wonderful gathering of math educators and mathematicians. Some interesting problems were posed to the secondary school teachers, which we were to solve with the help of interactive geometry software. Here are three of the problems. It was quite interesting to me to find that the second and third are in fact related to the equiangular points problem!
1. The burning tent. You're at point A, with an empty bucket. Your tent is on fire at point B. What is the shortest path from A to B if you want to stop at the straight river L to fill your bucket? You can move P to see what happens.
This problem was familiar to me (I first encountered it many years ago in Chakerian, Crabill, and Stein's Geometry: A Guided Inquiry.) If you have not seen it before, you should definitely work on it.
2. Island camping. Same problem, but this time you are on a circular island. You can move P. Look for the minimum total distance, as well as the maximum.
(Download the GeoGebra file)
I don't have a proof, but it seems like the optimal point in this case is an equiangular point for ∆OAB on the circle. In other words, a point from which ∠APO=∠OPC. (It is easy to show that this is the point for which angle of incidence equals angle of reflection.) You can verify this by showing the locus of equiangular points.
3. Another triangle center. Given a triangle ABC, where is the point P for which PA+PB+PC is minimum?
It turns out that it is the point mentioned above, where the triangle appears to be equilateral. (In other words, ∠APB = ∠BPC = ∠CPA.) This point is called the Fermat point.
The figure below shows all the equiangular points for a triangle. The Fermat point is at the intersection of all three curves inside the triangle.
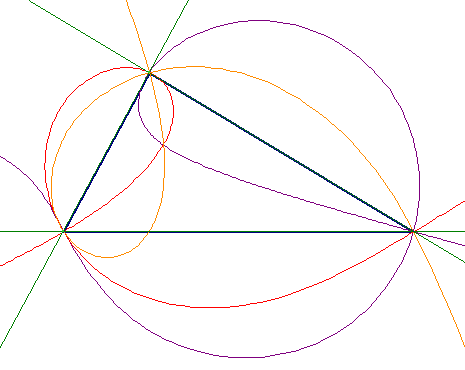
There is a construction of the Fermat point that does not use these loci. Can you find it?
