www.MathEd.page/angles
Adapted from Geometry Labs, by Henri Picciotto
Angles Around a Point
Equipment: Pattern Blocks
Place pattern blocks around a point, so that a vertex (corner) of each block touches the point, and no space is left between the blocks. The angles around the point should add up to exactly 360°.
For example, with two colors and three blocks you can make this figure:
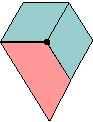
Use the chart below to keep track of your findings.
- Every time you find a new combination, circle the appropriate number on the list below.
- Cross out any number you know is impossible.
- If you find a possible number that is not on the list, add it.
Since the two-colors, three-blocks solution is shown above, circle that one first.
| Colors |
How many blocks you used |
| all blue |
|
| all green |
|
all orange
|
|
| all red |
|
| all tan |
|
| all yellow |
|
| two colors |
|
| three colors |
|
| four colors |
|
| five colors |
|
| six colors |
|
How many solutions are there altogether? __________
Discussion
- Which blocks offer only a unique solution? Why?
- Why are the tan block solutions only multiples of 4?
- Explain why the blue and red blocks are interchangeable for the purposes of this activity.
- Describe any systematic ways you came up with to fill in the bottom half of the chart.
- How do you know that you have found every possible solution?
- Which two- and three-color puzzles are impossible, and why?
- Which four-color puzzles are impossible, and why?
- Why is the five-color, eight-block puzzle impossible?
- Which six-color puzzles are impossible, and why?

