Definitions and Assumptions
For a definition of reflection, the construction assumptions, and the assumption that reflections preserve distance and angle measure, see TCS1 pp. 3-4 or TCS2 pp. 2-3
It follows readily from the definition of a reflection that a reflection is its own inverse.
An additional assumption is that reflection reverses the orientation of three non-collinear points (clockwise to counterclockwise, or vice-versa.)
Two more definitions:
- Given a vector `\vec V`, the image of a point A under a translation by `\vec V` is a point B such that `\vec {AB}` = `\vec V`.
- Given a point O and an angle `\theta`, the image of a point A ≠ O under a rotation with center O and angle `\theta` is a point B on the circle centered at O with radius OA, such that `\angle`AOB = `\theta`. The image of O is O.
Preliminary Results
Theorem 1: Three non-collinear points and their images determine a unique isometry.
The proof relies on the construction assumptions, and can be found on page 10 of IP.
Theorem 2: Any isometry is equivalent to the composition of at most three reflections.
Because of Theorem 1, it is sufficient to prove that given two congruent triangles, one is the image of the other in a sequence of at most three reflections. If the triangles are congruent, they must satisfy SSS. Follow the proof of the SSS theorem, which is based on reflections, to establish this result (TCS1 p. 6, or TCS2 p. 5. There is also a less rigorous argument on p. 11 of IP.)
It follows that given any two congruent figures, one is the image of the other in the composition of at most three reflections. We will attempt to identify the isometry that will take one to the other by analyzing all the cases: one reflection, two reflections, three reflections.
Of course, if an isometry consists of a single reflection, it is a reflection.
Two Reflections
(See IP p. 7, #1-5 and p. 12 #1-2.)
Two Parallel Lines
Theorem 3: The composition of two reflections in two parallel lines is a translation whose vector is perpendicular to the lines, with direction from the first line towards the second, and magnitude equal to twice the distance between the lines.
This result is illustrated in the figure below. You can convince yourself that the theorem makes sense by moving the original (orange) polygon anywhere, and seeing how the final image (indigo) behaves.
Click on check box 1, then 2. Use the definition of reflection and the distributive law to prove the theorem.
One consequence of this theorem is that only the slope of the lines, and their distance from each other matters to the final image, as you can see in the figure below. We will use this result in subsequent proofs.
You can move the pair of parallel lines by grabbing the o. You'll see that while the intermediate image changes, the final image does not.
Another consequence is that any translation is the composition of two reflections in parallel lines, as you can see in the figure below.
Click on the check boxes in order. How were the reflection lines created?
It follows also that translations preserve distance and angle measure.
After two reflections, orientation has been reversed twice, so it is back where it started. Therefore:
Corollary: Translations preserve orientation.
Two Intersecting Lines
Theorem 4: The composition of two reflections in intersecting lines is a rotation centered at the intersection, with angle equal to double the angle between the lines, going from the first line towards the second.
Click on the "Show" checkbox. The proof is similar to the one for Theorem 3.
It follows that only the intersection point, and the angle between the lines matters to the final image, as you can see in the figure below. We will use this result repeatedly in subsequent proofs.
Use the slider to confirm: the intermediate image moves, but the final image does not.
Therefore any rotation can be decomposed into two reflections, across lines that meet at the center of rotation, making an angle that is half the angle of rotation.
Corollary: Rotations preserve distance, angle measure, and orientation.
Three Reflections: Parallel or Concurrent Lines
Before reading further, take a moment to find all the ways three lines can be arranged. (See IP, p. 12 #3.)
We will start with the case where all three lines are parallel.
Three Parallel Lines
The figure shows the composition of three reflections, consecutively in lines e, f, and g. To keep notation at a minimum, we will call the reflections simply E, F, and G respectively, and the composition G F E (writing from right to left, as is customary for composition.) We will stick to these conventions for the rest of this paper.
The result of the first two reflections (F E), as expected, is a translation.
Use the slider. The translation is unchanged as we move lines e and f, keeping them parallel to g, without changing the distance between them. So we have:
G F E = G F' E'
If we stop when f' coincides with g, we can write:
G F E = G F' E' = G G E'
But G G is the identity! So we have:
G F E = G F' E' = G G E' = E'
Theorem 5: The result of the composition of reflections in three parallel lines e, f, g is a reflection in the image of e in a translation whose vector is perpendicular to the three lines, has magnitude equal to the distance between f and g, and whose direction is from f to g.
Three Concurrent Lines
A similar argument leads to:
Theorem 6: The result of the composition of reflections in three concurrent lines e, f, g is a reflection in the image of e in a rotation whose center is the lines' point of intersection, and whose angle is the angle between f and g.
Use the slider to confirm.
Glide Reflection
Before proceeding to the remaining cases, we introduce the glide reflection.
- Given a line b and a vector `\vec V` parallel to b, the image of a point A under a glide reflection with vector `\vec V` and reflection line b is the image of A under a composition of a translation by `\vec V` and a reflection in b.
Although it is not one of the rigid motions mentioned in the Common Core State Standards, the glide reflection is worth knowing about. It is particularly useful in analyzing symmetries in friezes and wallpapers, and it occurs in nature, for example in the footprints left when walking on the beach.
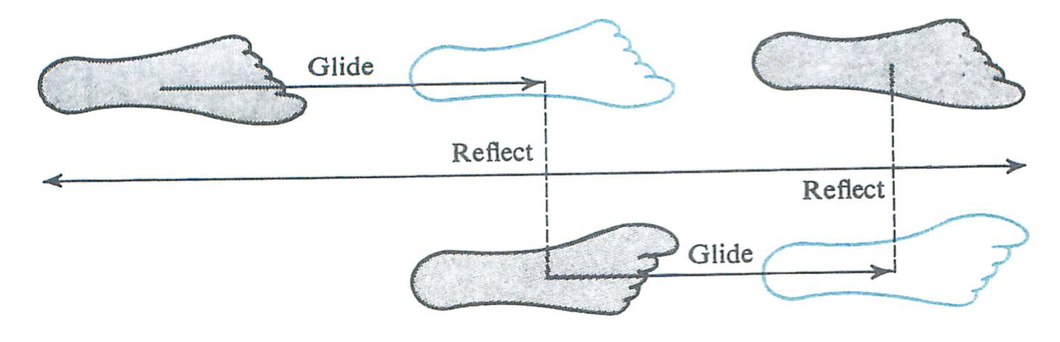
Figure from Richard Brown's Transformational Geometry.
(Introduction to the glide reflection. See also IP pp. 3 and 5.)
What we will see in the next section is that the composition of three reflections in all remaining cases is a glide reflection. The following theorem will be helpful.
Theorem 7: The translation and reflection that constitute a glide reflection can be performed in either order.
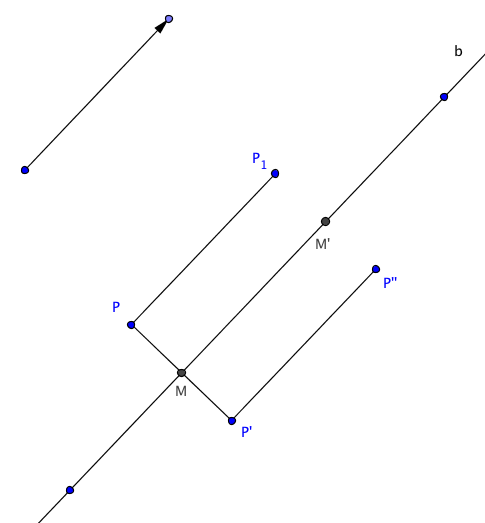
This follows readily from the definitions and properties of reflection and translation. Let b be the line of reflection. Let the image of P under the reflection be P'. Let the images of P and P' under the translation be P1 and P". We need to show that P" is the reflection of P1 in b, in other words that b is the perpendicular bisector of P"P1. Let M be the midpoint of PP', and M' be its image under the translation. Since translations preserve angles, P1, M', and P" are collinear, and PP" is perpendicular to b. Since translations preserve distance, M' is the midpoint of P1P". QED.
Three Reflections: Remaining Cases
There are three cases involving parallels and a transversal, depending on the order of the reflections.
Transversal First
The figure shows the composition of reflections in lines a, b, c in that order. Since orientation has been reversed, it cannot be a translation or rotation. It is visually obvious it is not a reflection. We will show it is in fact a glide reflection.
- Can you picture the glide reflection that takes the pre-image (0) to the final image (3)? It may help to move the original (orange) triangle and see the effect it has on the final (indigo) image. Remember: you can reset the figure by clicking the icon at the top right.
- Click checkbox 0. The red line (g) seems to be the glide reflection line. Can you guess how it is related to the original three lines?
- Click checkbox 1. d is perpendicular to b and c through the intersection of a and b.
g is parallel to a, and passes through the intersection of d and c. - Click checkbox 2. We now use algebra. Insert the identity in the expression C B A, then use the associative law (which always applies to the composition of functions):
C B A = C (D D) B A = (C D) (D B) A
Note that (C D) and (D B) are rotations that do not change when the lines are rotated simultaneously around their intersection through the same angle. - Use the slider. We rotate lines c and d simultaneously, around their intersection, until c' = g. The image of d is f. That keeps their composition unchanged, so (C D) = (G F).
Likewise lines d and b until b' = a. This time, the image of d is e, and we have (D B) = (E A).
This allows us to rewrite our expression:
(C D) (D B) A = (G F) (E A) A = G F E (A A) = G F E
But F E is a translation whose vector is parallel to G, so G F E is a glide reflection! - Click checkbox 4 to see the desired result: C B A is indeed a glide reflection.
Transversal Last
This time, we reflect in the transversal last. We will follow a similar path for the proof: click the checkboxes and use the slider.
Note that there is a pleasing symmetry with the "Transversal First" argument.
Transversal Second
We reduce this case to the previous one: by rotating b and c simultaneously around their point of intersection, we turn this into the "transversal last" setup.
General Case
The lines of reflection are not concurrent, and no two of them are parallel.
Once again, we reduce this to "Transversal Last".
- This time, we rotate b and c simultaneously around their point of intersection, until b's image is parallel to a. (Use the slider).
- When you click checkbox 2, you get a version of the final figure of "Transversal Last". You may review that proof now, if it would help.
- When you're ready to accept its application to this case, click checkbox 3 to just see the final result.
We have worked through all the cases, so this concludes our proof!
Summary
- Here is a summary of what is admittedly a lengthy argument.
- - An isometry is uniquely determined by three non-collinear points and their images.
- - Any isometry is the composition of one, two or three reflections.
- - The composition of two reflections is either a translation or a rotation.
- - The composition of three reflections is either a reflection or a glide reflection.
- Therefore:
Fundamental Theorem of Isometries: Any isometry of the plane is a reflection, a translation, a rotation, or a glide reflection.
Pedagogical Implications
- I have taught this material to 11th and 12th graders in my Space course. (In fact, the simple and elegant proof of the general case for three reflections was suggested by Jacob Regenstein, then a student in that class.) I did not do this in one day or one week, but over many weeks, after and alongside other relevant work:
- - An in-depth unit on symmetry, including frieze and wallpaper symmetry, which helped students develop their visual familiarity with the isometries.
- - A high-school-appropriate introduction to group theory, which helped prepare students for the algebraic arguments that facilitate the three-reflection proofs.
- - A unit on how to compute the coordinates of the image of a point under various transformations, starting with complex numbers, and continuing with matrices.
- A sense of the sequencing I used is suggested by this approximate syllabus.
Because this material is not included in the already bloated Common Core State Standards, it is not likely to find its way into many classrooms. Still, it makes sense to me as part of a Precalculus course, or a Year 4 elective alternative to Calculus. (My views on the Common Core.) NCTM's call for change in high school math (in their Catalyzing Change document) does open the door to more varied offerings in 11th and 12th grade math. Perhaps this material belongs in one such course.
However, it should not be taught in the sequence presented here: for example, the composition of two reflections, and the basics of glide reflections should be introduced early on. (In fact, those ideas could even be included in a geometry class.)
Note that understanding orientation is very helpful in thinking about this: an odd number of reflections must reverse orientation, so it cannot be a rotation or translation. An even number of reflections must preserve orientation, and so it cannot be a reflection or glide reflection. Extensive discussion of orientation early on helps develop students' feel for the isometries.
Having taught this material both with and without interactive geometry software, I must warn you that you are not likely to be successful in reaching many students if you try to do it without. All these ideas became vastly more accessible when I started using Cabri (and now GeoGebra.)
Finally, I think this material is of great interest to teachers, which is why I include it in my summer workshops when I can.