/puzzles
| Visit Henri Picciotto's Math Education Page. | Send me e-mail . |
Geometric Puzzles in the Classroom
Tetrarcs and Pentarcsby Brendan Owen | |
|
For a little background and context, see | |
|
A while ago I designed a general definition file for polyforms which consists of:
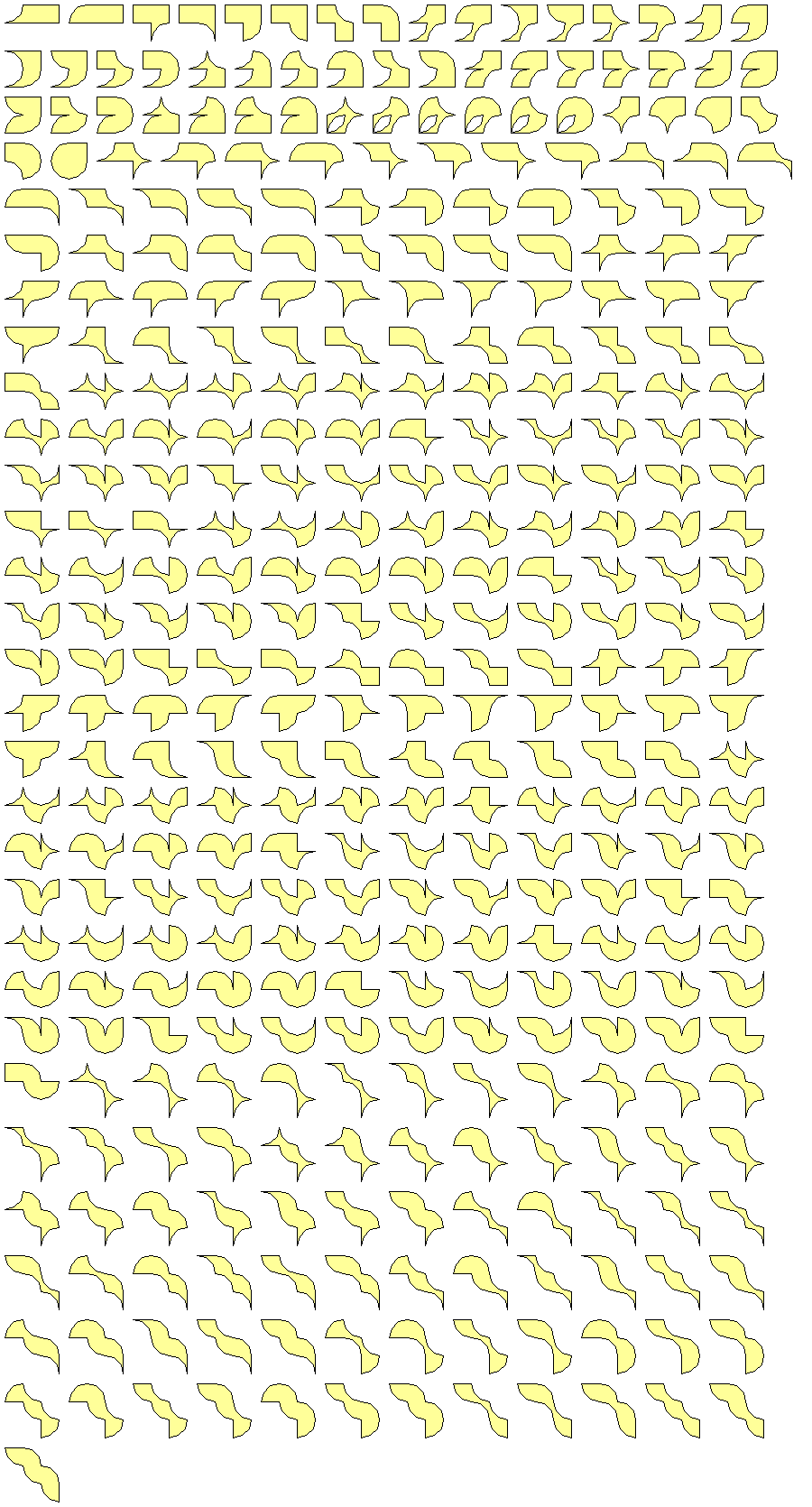
"Growing" the (n+1)forms is done by adding base units to the (n)forms edges, normalizing, sorting and removing duplicates. In order to be able to use the program for the polyarcs, I represented the arcs with pairs of straight lines. Here are some of the results of my search: Number of polyarcs: n n-arcs 1 2 2 7 3 22 4 93 5 364 6 1734 7 8246 8 41043 9 206602The tetrarcs: 
The pentarcs: |
|