I have found geometric puzzles to be an excellent springboard for mathematics lessons, as they are interesting to both students and teachers. They lend themselves to teaching some specific concepts as well as to building students' spatial sense and problem-solving skills. Moreover they show to a wide range of learners that exploring mathematics can be rewarding, irrespective of any "practical" application. As a result, geometric puzzles have consistently found their way into my classes, my workshops, and my books. In fact they were how I first broke into print.
There are many geometric puzzles that can be used in the classroom, such as for example tangrams and rep-tiles as presented in my book Geometry Labs, or Rubik's cube. In this article, I will concentrate on polyforms.
One-inch graph paper is useful for many of the activities described here.
Polyforms
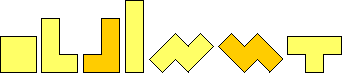
Polyforms are the shapes you get by combining multiple copies of a given "form" (usually copies of a given polygon, attached to each other edge-to-edge.) The best known example are the polyominoes, which are created by combining squares, and the best known among polyominoes are the shapes obtained by combining four squares. Those shapes are known as tetrominoes, and are the basis of the electronic game of Tetris.

If you think of them as puzzle pieces you can pick up and turn over, there are five tetrominoes, as shown in the figure. (The shapes can be remembered with the mnemonic "square lint".) But if the pieces are one-sided and have to remain in the plane (as in Tetris), there are two more:
Polyominoes, by Solomon W. Golomb (the man who coined the word,) appeared in 1964. It is out of print, but the revised and expanded second edition: Polyominoes: Puzzles, Patterns, Problems, and Packings, is available from Princeton University Press, NJ, 1994. This is the polyform bible.
Several of Martin Gardner's books of Scientific American articles include articles on polyforms and related topics in recreational mathematics. (Look for polyaboloes, polycubes, polyhexes, polyiamonds, and polyominoes in the Gardner Index.)
The Journal of Recreational Mathematics (at university libraries) also includes articles on this topic, as does Michael Keller's games and puzzles 'zine.
On the Web, many sites devote substantial space and links to polyforms -- many more than I have time to keep up with. A search will turn them up. A few places to start are:
- Ed Pegg's Mathpuzzle.com
- Kate Jones's Kadon Enterprises
- Michael Keller's Counting Polyforms
In the classroom:
- My book Polyomino Lessons has about 40 pages of puzzles and activities on this subject. (It is a free download for your non-commercial use.)
- Fourteen activities in my book Geometry Labs are dedicated to polyominoes.
One of those, on polyomino perimeter as a function of area, is summarized on this Web site, in my article "A New Algebra". It is an activity which seldom fails to engage. It works well on the first day of an 8th or 9th grade algebra course to introduce such ideas as the deep connections between geometry and algebra, and the different representations of functions.
- A set of polyomino puzzles that did not fit in the book are available here to print and duplicate:
Tiling Rectangles with PolyominoesTeacher notes: An entire chapter of Golomb's book is devoted to this topic, and it mentions a number of unsolved questions. For example: the smallest number of a given polyomino that can be used to tile a rectangle is called the order of the pentomino; it is not known whether there are any polyominoes with odd order.
To be able to work on the puzzles on the worksheet, students need to know the names of the tetrominoes and pentominoes. (You may duplicate page 54 of Geometry Labs, or if you don't have the book, print and duplicate this Polyomino Names Reference Sheet.) A hint for #2 is that (surprisingly) the smallest rectangle that can be tiled with the Y pentomino is 5 by 10.
Pentominoes
Pentominoes are made of five squares, and are the subject of many, many classic puzzles.
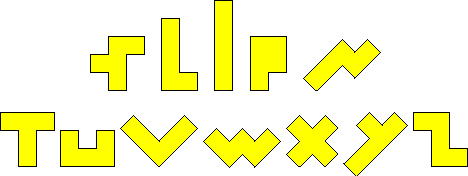
(The mnemonic "FLIP'N TUVWXYZ" is helpful in finding out quickly which piece is missing in an incomplete set.)
The earliest pentomino puzzle I know of is in H. E. Dudeney's 1919 book, The Canterbury Puzzles (available from Dover Publications), pages 119-121. In Arthur C. Clarke's science-fiction book Imperial Earth (Ballantine Books, 1976), Chapter 7 is mostly about a ten-year-old's exciting encounter with pentomino puzzles. "What had at first seemed merely a childish game had opened endless vistas and horizons... there was something strange here, something magical. It was Duncan's first glimpse of the power of intuition..."
What rectangles can be simultaneously covered with pentominoes from one set? Find the answer in Simultaneous Pentomino Rectangles.
In the classroom:
- Pentominoes home page
- Sample Pentomino Labs.
- Working with Pentominoes, by Henri Picciotto. A book of pentomino lessons, keyed to the Common Core State Standards. It is available from Didax, and comes with an eBook version on DVD. The latter can be projected on a screen or interactive whiteboard, and includes manipulable pentominoes. It is a good companion to the puzzle books described below, as it makes the curricular connections explicit. They also sell a downloadable PDF, which would be convenient to print specific pages for classroom use.
- I have brought pentominoes to many kids and teachers through my book: Pentomino Activities, Lessons, and Puzzles. It includes hundreds of puzzles and dozens of lessons, and you can find material in it for pretty much any grade level. It has been in print continously from 1984 to 2012, and has generated fan mail from inner city kids in New Haven and migrant farmworkers' children in the San Joaquin Valley, plus an eloquent missive from a second grader in Tennessee who found an error in the solutions. It is going out of print, but may still be available from McGraw-Hill.
- I also created The Math Machine Pentomino Puzzles (1984) and Pentomino Pattern Cards (a subset of same). Those too are going out of print, but they may still be available from Carson-Dellosa.
(Where to get these materials.)
You can freely download three of the books mentioned above for your non-commercial use — Pentomino Puzzle Books.
Also on this website: you can play with virtual pentominoes.
Supertangrams
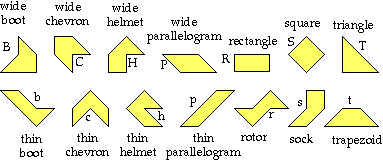
Supertangrams are the polyforms obtained by combining four unit isosceles right triangles snugly in every possible way. There are 14 supertangrams. Martin Gardner wrote about them under the name "tetraboloes" (in The Mathematical Magic Show, chapter 11). They are also known as "tetratans", a word I coined. The "supertangram" name obscures the fact that the figures are polyforms, but it does reveal the geometric connection with the classic tangram puzzle: both tangrams and supertangrams are made from right isosceles triangles, and in fact all three medium-sized tangram shapes are also supertangrams.
Supertangram puzzles are more difficult than pentomino puzzles, and much more difficult than tangram puzzles. In SuperTangrams for Beginners 2, I proposed a notation for the 14 pieces. (Mnemonic: "BaCH, PRouST", and/or "BeaCH PReSTo".)
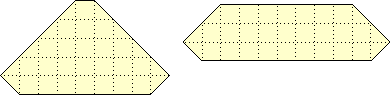
A 14-piece rectangle is not possible (see Gardner). The proof generalizes to any rotationally symmetric shape (not, as Gardner claimed incorrectly, to bilaterally symmetric shapes). In 1989, I found and published two bilaterally symmetric convex 14-piece shapes:
I also found another symmetric 14-piece shape, as did Ed Pegg (see this page on Michael Keller's site.) Finally, Miroslav Vicher found six other 14-piece convex figures through a computer search.
In the classroom:
- I sell plastic supertangrams. More info: Supertangrams home page.
- Print and duplicate the supertangram Labs. This is a whole unit, starting with the discovery of the shapes, including many puzzles, and ending with a rich lesson on similarity and the square root of two.
- I have "written" five books of supertangram puzzles. They are available for free on this website.
Polyarcs
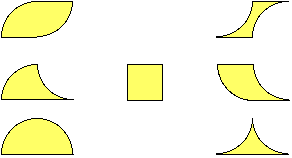
Consider the two pieces that are created by drawing a quarter circle with radius one, centered at the corner of a unit square. Call these pieces monarcs. Their average area is 1/2.
Two monarcs can be combined to create diarcs in seven distinct ways. The average area of the diarcs is 1.
The total area of all of the monarcs and diarcs is 8. They can be combined into a 2x4 rectangle, or a pleasingly symmetric curvilinear figure:
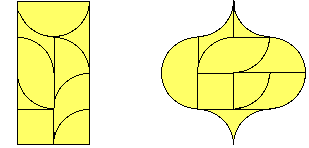
There are 22 triarcs, with average area 1-1/2, and total area 33. In combination with the diarcs the area would be 40. All the usual polyform questions can be asked: What symmetric shapes can be constructed using all or some of the triarcs? All or some of the diarcs and triarcs?
In contrast to polyominoes, which have been researched extensively, little is known about polyarcs. If you or your students discover interesting polyarc figures, please send me copies of your solutions! Several puzzle enthusiasts did just that, as you can see below.
More on polyarcs:
A zipped Word file of the monarcs and diarcs, by Alex Link. Using Word's drawing tools, they can be dragged, flipped and rotated into interesting shapes.
Hundreds of monarc/diarc figures, by Alex Link.
Hundreds of solutions to diarc puzzles, by Bernd Karl Rennhak.
You can purchase a beautiful plastic set of diarcs and triarcs from Kadon Enterprises.
Diarcs and Triarcs, by Michael Keller.
Tetrarcs and Pentarcs, by Brendan Owen.
Polyarc numbers on the Online Encyclopedia of Integer Sequences.
In the classroom:
- A Polyarcs Lab for your students. Prerequisites: Students need to know how to find the area and perimeter of a circle.
- A related activity: Leonardo's Areas
- A blog post by Meghan Lee: Polyarcs in the Classroom