Geometric Definition
Definition: A parabola is the set of points in the plane that are equidistant from a point (the focus) and a line (the directrix.)
The following exercise should help convince you that this definition yields the parabolas you are familiar with.
Exercise: Given a focus at (0,1) and a directrix y=-1, find the equation of the parabola. How to do it: draw a figure showing a generic point P on the parabola, with coordinates (x,y). Calculate its distance to the focus, its distance to the directrix, set those equal, and simplify. Or, for a more general result, do this exercise for a focus at (0,f) and a directrix y=-f.
Construction
Given the focus (F) and directrix (d), here is a method to construct any number of points on the parabola: choose a point T on d. Construct the perpendicular bisector of TF. Construct the perpendicular to d through T. The intersection of these two lines (P) is a point on the parabola. (Make sure you understand why.)
Exercise: With the help of dynamic geometry software, construct P as outlined above, then trace P as T moves, or create its locus, which is the parabola. Here is the step-by-step process in GeoGebra (I recorded this at geogebra.org/classic.):
Reflection Property
A light ray originating at the focus will be reflected on the parabola and continue in a direction parallel to the axis of symmetry. Likewise, a light ray coming in parallel to the axis of symmetry will be reflected to hit the focus.
That this works is readily proved using the above construction, if you assume a basic fact from optics: the angle of incidence equals the angle of reflection. The key to the proof is realizing that MP must be tangent to the parabola. Indeed, assume MP intersects the parabola at P and another point P'. Because P' is on MP, it is equidistant from F and T. Because it is on the parabola, it is equidistant from F and d, so if T' is the foot of a perpendicular from P' to d, we have P'T = P'F = P'T'. But the only way for P'T to equal P'T' is for T' to be T. Therefore P' is P, and MP is tangent.
Exercise: Prove the reflection property of the parabola, assuming that the angles of incidence and reflection are determined with respect to the tangent to the parabola at the point of incidence.
The reflection property suggests this construction of sorts:
You can move point T on the directrix and see how the perpendicular bisector of TF moves. Click "Show trace" and/or "Show envelope". (The curve that is tangent to all these lines is called their envelope. In some situations, such as this one, GeoGebra is able to calculate and display the envelope from the definition of the lines.)
Download the GeoGebra file
This property is of course the basis of many applications (headlights, flashlights, satellite dishes, radar...) For example, here is a diagram of how this works in a reflector telescope:
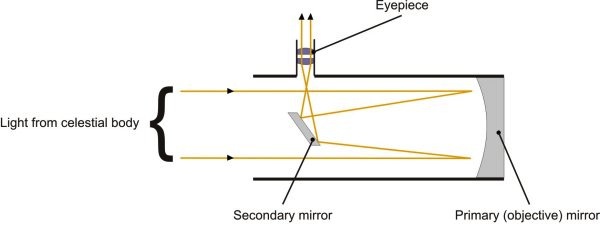
The primary mirror is parabolic, reflecting the parallel rays to the focus. The secondary (flat) mirror redirects this towards the eyepiece.
All Parabolas are Similar
Like squares and circles, unlike rectangles and ellipses, all parabolas are similar. They cannot be "pointier" or "wider". They all have exactly the same shape, which appears "pointier" from afar, and "wider" when looked at in the neighborhood of the vertex.
Unfortunately, many of us have misled many students by implying otherwise: we often claim that changing the value of a in the formula `y=ax^2` changes the shape of the parabola. In fact, many teachers believe this to be true. Here are four types of arguments to show it is a misunderstanding.
- Algebraic Argument:
- `y=ax^2`
- `ay=a^2x^2`
- `ay=(ax)^2`
- In other words, in the equation y=x2, both x and y have been multiplied by the same number a. The parabola is scaled with no distortion.
- Here is another version of the same argument. Scale the graph of `y=x^2` both vertically and horizontally by a factor of 1/a:
- `y=1/a*(ax)^2`
- Simplify: `y=ax^2`
Geometric Argument:
Since the directrix is infinite, moving the focus has no effect on the parabola's shape. It is merely zooming in or out on one shape.
- Visual Arguments:
- Same equation, apparently different shapes:
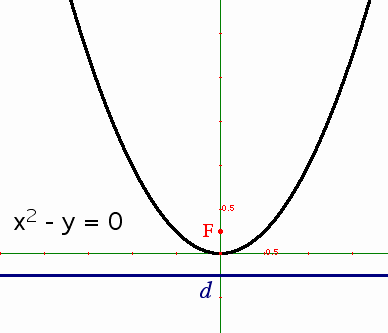
- (Dan Bennett suggests a dramatic illustration of this: make a transparency of a figure like the one above. Project it. Use another transparency to trace a piece of the projection, like the one below. Compare the two transparencies, which seem to have very different shapes, but clearly must represent the same equation. The same approach works on a document camera: place the original next to the projected image of a photocopy of itself.)
-
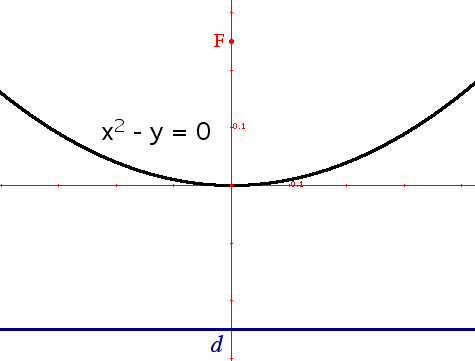
- In the applet below, click on the magnifying glass icon to switch between the Zoom In and Zoom Out tools. Select either one and click on or near the origin, and see how the same parabola's shape appears to change.
- Conversely, look at how different equations can yield the same shape:

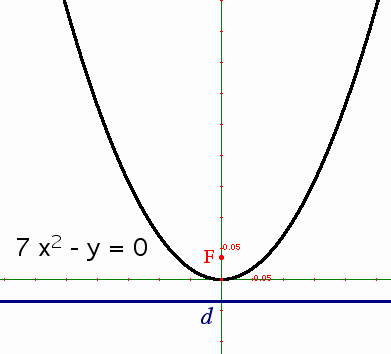
- In fact, you can see for yourself: in the applet below, drag the axes' unit (the "1" on the x-axis) left or right, and watch the `a` in the equation change while the parabola's shape remains absolutely constant.
Transformational arguments
Rachel Chou points out that to describe a parabola uniquely, you only need one piece of information: the distance between the focus and the vertex, or the distance between the vertex and the directrix, or the distance between the focus and the directrix. Likewise, a single measurement is sufficient to define a square (the side, the diagonal, the perimeter, or the area). A single measurement defines a circle (radius, diameter, ...). In contrast, a rectangle requires two descriptors (length and width, or one side and a diagonal, and so on.) Thus, you can create a different-shaped rectangle by multiplying length and width by different numbers. The same applies to ellipses and hyperbolas. But you don't have that option for squares, circles, or parabolas!
In this illustration, you can show that any two parabolas are similar by translating the first, and then dilating it, so that the final image is superposed on the second. (Use the translate and dilate sliders in order.)
Download the GeoGebra file
Geometer's Sketchpad file, by Rachel Chou, who suggested showing finite "cups" to make similarity more obvious.
Finally, in this illustration you can move the parabolas by dragging their vertices. You can change their respective a's by using the sliders. One parabola is always the image of the other in a single dilation — no translation needed! (Of course the challenge in creating this construction was figuring out where the center of dilation needed to be!)
Download the GeoGebra file
A worksheet on Parabola Similarity. (Requires GeoGebra or other dynamic geometry software.)