Blog Posts
Here are links to posts on my Math Education Blog that you might find interesting.
If you are so moved, you may comment on the posts, and/or subscribe to the blog.
Geometric Construction
In my critique of the Common Core State Standards, I complain about the fact that they continue the long term shrinkage of geometry in the US secondary math curriculum. In particular, geometric construction is limited to a few standard basic techniques. Fortunately, this is countered by the growing availability of geometric construction tools (such as Cabri, Sketchpad, GeoGebra, and others). Moreover, a pedagogically much healthier outlook is embedded in geometric construction games. In those, you are given a starting configuration, a limited set of tools, and a construction goal. In this view, geometric construction is a puzzle environment. I link to three such games, and to my own writing and curriculum on the subject, in this post.
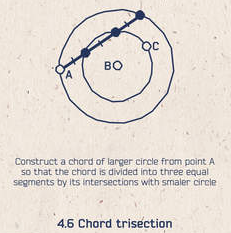
In addition to enhancing perseverance in problem solving, work on geometric construction strengthens one's grasp of geometry, obviously. But the benefits also expand to such topics as conic sections. (Read about the geometry of the conic sections on my Web site, starting here.)
Geometric Series, Geometrically!
Speaking of geometric construction: I wrote a post about geometrically constructing the sum of an infinite geometric series, if the common ratio is strictly between 0 and 1. (The construction would not work if the absolute value of the ratio is greater than 1. I believe a similar construction might work if it is strictly between -1 and 0. Let me know if you find it!)
I imagine this could be expanded into an Algebra 2 or Precalculus lesson, one which would combine a review of important ideas from geometry with new work on infinite series. If you create such a lesson, let me know! In any case, even if it does not find its way into your classroom, look it up, because it is a nice construction which connects many topics. Click here.
Warm-Ups
When I was teaching high school, I typically started the period with some time for students to go over homework with each other in groups. In course evaluations, they consistently let me know that this was a valuable component of my class routine, one which they deemed essential to their learning. Typically, homework was on old material, not yesterday's lesson. There are many excellent reasons to "lag homework", which I explored in this post back in 2013. Thus, for my classes, going over homework served pretty much the same purpose as standard warm-up problems, which are typically seen as a way for students to start working immediately, while reviewing old material.
However, in a recent talk by Scott Farrand, I learned about a whole nother approach to warm-ups. What Scott does is devise the day's warm-up problem as a short but challenging (or at least interesting) problem that helps prepare students for the day's lesson. Obviously, the warm-up must rely on old material, but the key is that it is not intended mainly as review. Instead, it is forward-looking, and tries to get students to wonder about the question that today's lesson will answer. He believes this is one key to effective lesson planning, and I have to agree. To read more about Scott's approach, and see an example, click here.

