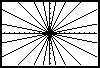
"Make These Designs" is an activity I have used in Algebra classes, over many years. It can be done with just about any electronic grapher. Its purpose is to reinforce students' understanding of the connection between the graph of a linear function, and the parameters m and b in the formula y=mx+b.
Students are given a set of designs, and they must create them on their electronic grapher. They should do this by entering functions of the form y=mx+b. The challenge is finding the right values of m and b. (Before reading on, you should try to do the activity yourself.) This activity is popular, as in many classes students see it as a break from the usual routine. As students show you partial results and ask you questions, you will have many opportunities to focus their attention on the underlying mathematics. When a question arises that is of concern to enough students, you may interrupt individual work for a whole-class discussion on the overhead.
Students need not solve the problems in any particular order. As they work on one figure, they may accidentally create another one. Allowing them to set their own path through the activity makes it more enjoyable, and gives them more ownership. It also makes it difficult to be competitive in an immature kind of way ("Which one are you on? I'm ahead of you."), allowing the students to concentrate on the mathematics.
It is important that students keep records of how each image was achieved, and that there be some small-group and/or all-class discussion of these records. Without such discussions, students may get through the activity, and not learn all they can from it, even if it appears to "go well". Some of the questions that you may ask during these discussions are:
- How do you make lines steeper? less steep?
- How do you make lines that go "uphill"? "downhill"?
- How do you make lines horizontal? vertical?
- How do you make parallel lines?
- How do you make a parallel to an uphill line to the left of the original? to the right?
- How do you make a parallel to a downhill line to the left of the original? to the right?
- How do you make a parallel to an uphill line higher up? lower down?
- How do you make a parallel to a downhill line higher up? lower down?
As they work on the problems, you should circulate among the students, prodding them to improve their designs. On the first figure, for example, you should encourage students to fill out the star figure, as they often fail to include lines that make an angle of less than 45 degrees with the x axis. (For an account of a similar activity and the questions that come up for students and teacher, see Magidson, 1992.)
Note the questions about left and right. It turns out that if lines are steep, as in the seventh and eighth figures, students often see the b parameter as moving the lines left or right, even though teachers see it as moving them up or down. Having the left-right discussion helps students see that changing the value of b has different effects on the x-intercept depending on whether the line is uphill or downhill, while it always affects the y-intercept the same way. In fact, this is a good opportunity to observe that b is the y-intercept. A discussion of how to find the x-intercept through symbol manipulation is a nice detour from this activity. This is a rather sophisticated level of discussion that you should not expect the first time students approach this activity -- however your own clarity on this can help you deal with their questions about moving lines left and right, and it does give you somewhere to go with the students who quickly master the basic ideas about slope and intercept.
Note also that students are asked to graph vertical lines. It is of course not possible to do it using the "y=" format. (Actually, it is possible, but not easy. Can you do it?)
Working at Many Levels
This activity is an example of an approach to curriculum that offers both access and depth in the same lesson. Access, because no one is frozen out of the activity: all students can understand the question, get started, and find a challenge to stretch their own understanding. Depth because there are many ways to increase the mathematical payoff and to keep even your strongest students challenged. (The slogan used in the Logo community to describe such curricula is "No threshold, no ceiling.")
Whether a given design is reproduced accurately is largely a matter of opinion. You may ask your students to capture the general look of a given figure, or you may ask for a nearly-exact replica. The former can be done by trial and error, and helps students develop a feel for the effect of m and b in a general sort of way. The latter requires a very clear understanding of the effect of the parameters, not to mention familiarity with the features of the electronic grapher. What level of competence you ask for depends on whether this activity is being used early or late in the process of learning about linear functions and their graphs. You may even expect different levels of accuracy from different students, as long as everyone is being challenged to move forward in their understanding. Certainly, for beginners, using about ten lines is sufficient to show understanding of the particular figure, even though the figure may include up to sixteen lines.
The graphs are mostly grouped in pairs, each of which tries to make a certain point, though of course your mileage may vary. The first two graphs show us lines with various slopes but the same intercept, however the intercept changes from the first to the second figure. The next two make the point about uphill versus downhill graphs, keeping the slope constant, but varying the intercepts. The next two address the special cases of horizontal and vertical lines. The next two raise the issue of moving lines to the left or right. The next two are an attempt to explore symmetry across the x and y axes. However you should avoid getting heavy-handed in demanding specific understandings right away. The central purpose of the activity is to advance students' grasp of the role of the parameters m and b. Any other learning is a bonus.
Making vs. "Noticing"
Many curriculum materials attempt to get the "slope-intercept" idea across by way of a lesson where students are asked to graph several lines, with the equations supplied by the curriculum writer. For example, they may be asked to graph y=x, y=2x, y=3x, and so on. Then they are asked "What do you notice?". The process is then repeated for y=x, y=x+1, y=x+2, and so on. I am sure that some students do figure out what is going on in this sort of lesson, but many do not. Part of the reason is that the graphing phase of the lesson does not engage the student intellectually: it's just a matter of entering the functions suggested by the worksheet. After looking at the graphs, students often do not notice what we want them to notice, and we are forced to give them sledgehammer hints. In effect students end up seeing the activity as one where they have to guess what the teacher is looking for. (For an account of what students sometimes "notice" in this context, see Goldenberg, 1988, 1991).
In contrast, "Make These Designs" forces students to think throughout the activity, because they are involved in a creative challenge. While this does not guarantee learning, it certainly helps, by providing an environment where the students (not the author of the worksheet) choose the formulas, and formulate the questions. This means that even if they are unable to readily answer these questions, at least they know what the questions are, which makes it a lot easier to hear the answers as they surface in group or class discussion, or in a teacher lecture. It is very difficult to hear the answers to questions one does not have, let alone understand them.
The essence of "Make These Designs" is the reversal of a traditional activity. Instead of asking for the graph given the equation, it asks for the equation, given the graph. This sort of reversal is a very powerful tool in the design of effective problem-solving activities. In fact, it can be said that one does not have a full understanding of most mathematical topics if one cannot comfortably reverse them. You do not fully understand addition if you do not understand subtraction -- otherwise how would you solve x + 1.234 = 5.123? You do not fully understand the distributive law, if you cannot factor anything. For a stimulating essay on the importance of reversal in the learning of algebra, see Rachlin, 1987. Understanding this can lead to a rethinking of all of one's teaching.
Assessment
I have often used the last figure as an "extra credit" problem if the activity is done as an introduction to m and b. On the other hand, I have used the last figure (or the whole sheet) late in the course to assess student understanding of slope and intercepts (both x- and y-). If you are using the activity as a wrap-up, students should write out full explanations of how some of the figures were created. It helps them cement their understanding, and it helps you assess it. To support students, you may give them a copy of the questions above, which can serve as a content checklist for a written report.
Extensions
The activity can easily be extended. For example, students can create their own designs, which can be printed or shown on the overhead for others to emulate. When they know some trigonometry, students can be asked to make the initial "starburst" design so that consecutive lines make a 15° angle with each other. In Algebra 2 or Precalculus, students can be asked to do a similar activity using quadratic, polynomial, rational, or trigonometric functions.
Conclusion
Using technology does not accomplish miracles, but it does provide an excellent context for the reversal of standard tasks, which yields powerful educational benefits. Still, the electronic grapher should not be the only way you address these concepts with your students. While the technology helps students' emerging understanding of the parameter/graph connection, this should not be mistaken for a full understanding of linear functions and rate of change. For example, while the slope of a line in a Cartesian graph is a very important way to think about the rate of change of the corresponding function, it is only one of the ways. Other representations, (tables of values, so-called real world situations, other visual representations such as function diagrams and manipulatives,) can also help students develop their understanding of these concepts. Do not put all your eggs in the technology basket!
Technical Notes
Originally, I used a graphing program I had written in the Logo language (Picciotto, 1990) for this activity. More recently, I have been using the TI-82, then TI-83, then TI-89 calculator. The given "window" makes each pixel be worth .2 both horizontally and vertically, and draws axes with ticks that are 1 unit apart. You may need to adjust these numbers for other electronic graphers, or create your own set of designs with the electronic grapher you use.
To get this many lines onto the screen may require using some of the special features of the calculator. On the TI-83/84, one can graph ten functions. To get more, students can use bracketed lists of parameters. (See the respective manuals for more information.)
References
Paul Goldenberg, "Mathematics, Metaphors, and Human Factors.", Journal of Mathematical Behavior 7 (September 1988), pp 135-173
Paul Goldenberg, "The Difference between Graphing Software and Educational Graphing Software." in Visualization in Mathematics, edited by W. Zimmerman and S. Cunningham. Washington, DC: Mathematical Association of America, 1991.
Sue Magidson. "What's In a Problem? Exploring Slope Using Computer Graphing Software." Proceedings of the Sixteenth PME Conference. Durham, NH, 1992, pp. 64-71.
Henri Picciotto. Logo Math: Tools and Games software. Terrapin, Inc, Portland, ME, 1990.
Sidney L. Rachlin. "Algebra from x to why: A Process Approach for Developing the Concepts and Generalizations of Algebra." In Wendy Caughey (Ed.), From Now to the Future. Melbourne, Australia: The Mathematical Association of Victoria, 1987, 213-217.
