To the Teacher
An essential foundation of secondary school geometry is the concept of angle. Many students do not have enough experience with angles when, at the beginning of a geometry class, we tell them how to use a protractor. Often, we are surprised at how difficult this idea is for many students. I have banged my head against that wall, repeating over and over to some students how a protractor is used, and eventually made some headway. But that was a frustrating approach. What I was missing was that the reason students have trouble is that it is difficult to measure something when you are not sure what it is. I developed a few lessons in order to build the intuitive foundation necessary for much of the work in a traditional geometry course. Of course, understanding angles is also necessary in reform-minded courses (such as the one I taught at the Urban School of San Francisco) and in later work in trigonometry.
The first two labs involve the use of Pattern Blocks. These were invented in the sixties by the Elementary Science Studies and can be found in zillions of elementary schools. My high school students sometimes affectionately call them "kindergarten blocks," and no, they do not find them offensive. See my article "Early Mathematics" for another use of pattern blocks, and a general discussion of manipulatives.
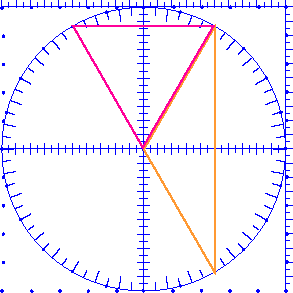
The third lab is more advanced, and involves the use of the circle geoboard. One version of this manipulative is the CircleTrig Geoboard, which I designed. It is available from Nasco. For more activities involving this tool, see The Ten-Centimeter Circle.
Of course, these labs are intended to complement, rather than substitute for, other approaches to these topics.
1. Angles Around A Point
Print and duplicate "Angles Around a Point".
Prerequisites: There are no prerequisites other than knowing that there are 360° around a point. I often use this lab on the first day of school.
Timing: To get the most out of this activity, you should plan to spend at least two periods on it. Students need time to understand what is expected, to search for many solutions, and to discuss their work as they go.
Teacher's Notes: There are many ways to solve the problem with, say, two colors and three blocks. It is enough to find one of the ways to circle that number.
The essential purpose of this lesson is to develop a rough quantitative sense of angle measurement without dwelling on the actual numerical values of the measurements. Make sure that all students are able to think (and therefore talk) about the activity at some level. However, if some students are ready for, and use, actual angle measurements, do not discourage that! Expect all students to get into this more formally in the next lab. When students start thinking that they have found every possible answer, you may reveal that there are 40 solutions altogether. This helps clarify things if there are actually many unfound solutions, but it may sabotage the quality of the discussion, since it takes away the opportunity to discuss Question E, which itself is an incentive to think about Questions F-I. Note that the impossible cases are of two types: logical and geometric. For example, solutions with four colors and three blocks are logically impossible. The cases that are impossible by virtue of the size of angles are more interesting from the point of view of the purpose of the lab.
2. Walking Convex Polygons
Print and duplicate "Walking Convex Polygons".
Prerequisites: none.
Teacher's Notes: The definition of convex polygon given here "A convex polygon is one where no angle is greater than 180°"is equivalent to this more formal one: "A figure is convex if the segment joining any two points on it lies entirely inside or on the figure." You can convince yourself of this by drawing a few pictures. It is not necessary to discuss this with your students; they will be glad to accept the equivalence without proof.
I do not believe in the widespread but absurd restriction that angle measurements must be less than 180°. We are talking to some students who can turn 360° on their skateboards, and to some who will soon be studying trigonometric functions. All of them live in a world where polygons can be nonconvex (consider the Star Trek insignia), and therefore include angles greater than 180°. Angles whose measures are between 180° and 360° are called reflex angles. You may add this word to your students' vocabulary, along with the better-known acute, right, obtuse, and straight, even if the word is not in the textbook you use. One of the theorems we commonly teach in geometry is about the sum of the angles in a polygon. The theorem still holds in the case of nonconvex polygons. Why limit this result with the artificial constraint that angles cannot measure more than 180°?
Some of the solutions to Problem 3 are quite difficult to find. It is not crucial for all students to find every one; you may ask them to work on this in groups. The main point of the exploration is to make sure students understand the definition of a convex polygon. Solutions to this puzzle can be beautiful, and you may want to display them on a bulletin board. Students who enjoy this challenge can be given additional constraints: It's possible to solve the puzzle using only squares and triangles. Another challenge could be to use as many tan pattern blocks as possible, or to find alternative solutions for each n-gon.
Make sure students understand the example of walking the trapezoid before letting them work on other figures. You may have a student demonstrate the walk in a figure similar to the one on the sheet, while another records each step on the board or overhead.
If the trapezoid instructions start in the middle of a side, as suggested in Question A, all turn angles must be included in order to finish the walk. This provides another reason for including the final turn in the "normal" walks that start at a vertex: This way, all versions of the walk include the same angles.
3. Angles and Triangles in a Circle
Print and duplicate "Angles and Triangles in a Circle".
Prerequisites: Triangle sum theorem, isosceles triangle theorem, exterior angle theorem.
Timing: This lab will take more than one period. Depending on how much discussion time you want to include, it could take up to three periods. It may not be necessary for all students to do the activity to the very end. If you think your students are "getting the picture" or are getting tired of this, you may interrupt them at the end of the last period you want to spend on this lab for a wrap-up discussion of what was learned.
Teacher's Notes:This is an extension that involves a lot of work and is probably most appropriate in a high school geometry course, in preparation for the inscribed angle theorem and its proof. However, this lab can be valuable even with less ambitious goals, such as developing a feel for the different types of triangles; providing an interesting experience in using the three theorems listed above; and discovering Thales's theorem (any angle inscribed in a half-circle is a right angle). In that case, it is sufficient to stop when most students have finished Problem 4, and perhaps Problem 5.
Problems 6 and 7 are mostly designed to prepare students for understanding the general proof of the inscribed angle theorem. Instead of doing them now, you may return to these problems later, perhaps with only circle geoboard paper rather than actual geoboards. You can even return to actual geoboards after students know the inscribed angle theorem, as an interesting way to practice applying the theorem.
